Delay distributions at the population level
Nowcasting and forecasting of infectious disease dynamics
Individual delay distributions
Let us consider an epidemiological process that is characterised by a discrete distribution \(f_d\).
Example:
\(f_d\): Probability of having incubation period of \(d\) days.
![]()
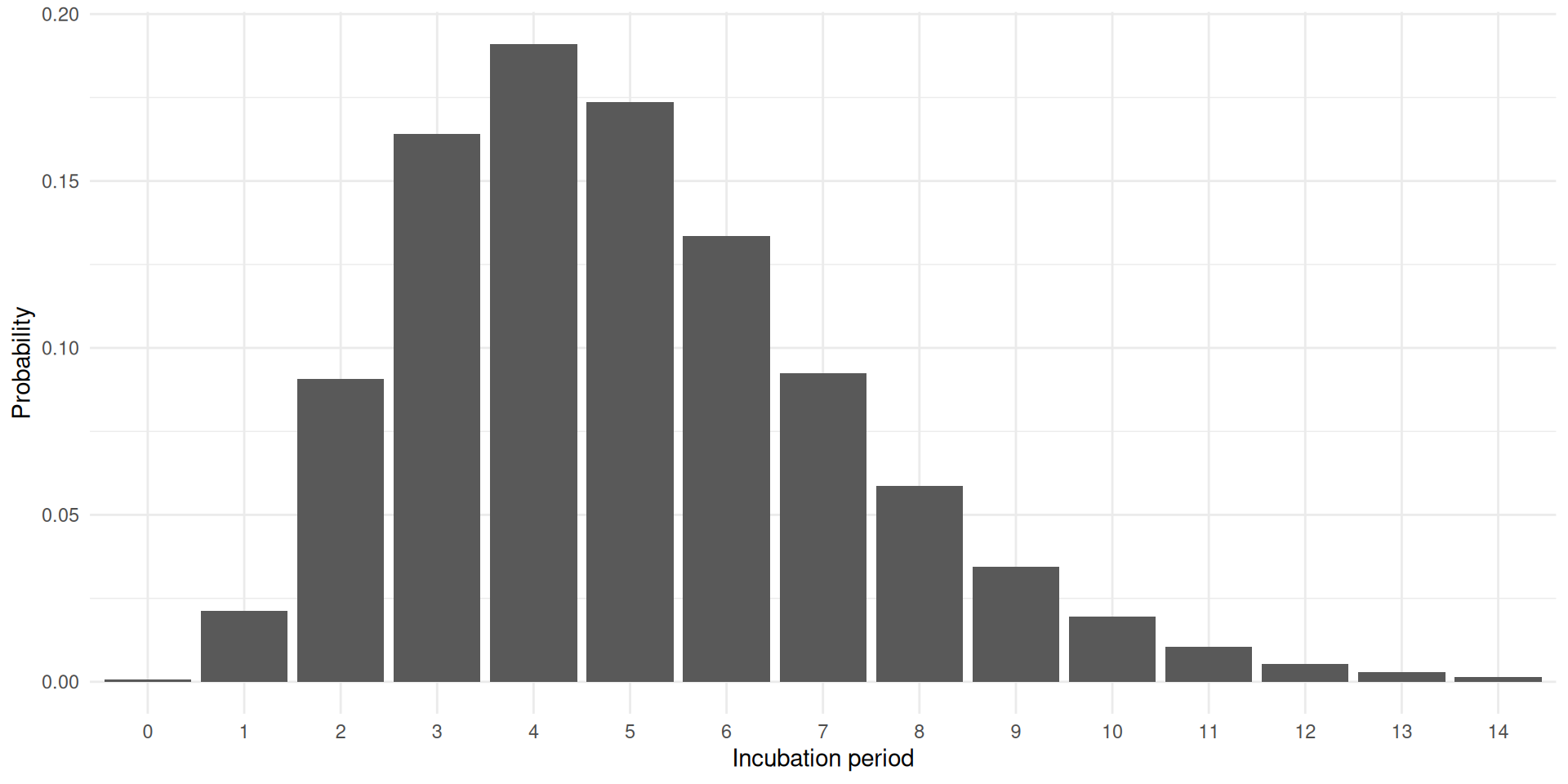
Population level counts
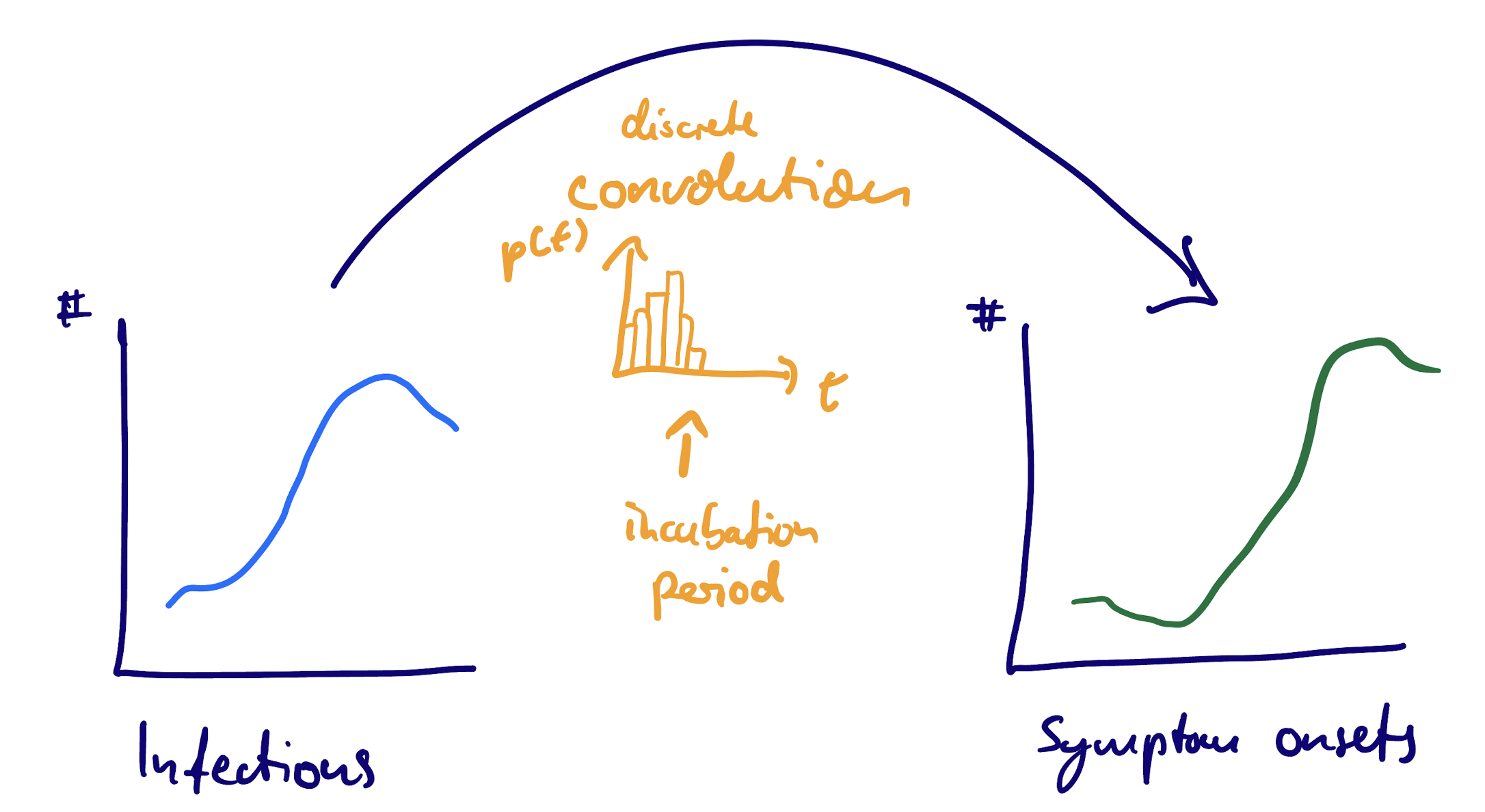
If the number of individuals \(P_{t'}\) that have their primary event at time \(t'\) then we can rewrite this as
\[
S_t = \sum_{t'} P_{t'} f_{t - t'}
\]
This operation is called a (discrete) convolution of \(P\) with \(f\).
We can use convolutions with the delay distribution that applies at the individual level to determine population-level counts.
Example: infections to symptom onsets
![]()
Why use a convolution, not individual delays?
- we don’t always have individual data available
- we often model other processes at the population level (such as transmission) and so being able to model delays on the same scale is useful
- doing the computation at the population level requires fewer calculations (i.e. is faster)
- however, a downside is that we won’t have realistic uncertainty, especially if the number of individuals is small
What if \(f\) is continuous?
Having moved to the population level, we can’t estimate individual-level event times any more.
Instead, we discretise the distribution (remembering that it is double censored - as both events are censored).
This can be solved mathematically but in the session we will use simulation.
Your Turn
- Simulate convolutions with infection counts
- Discretise continuous distributions
- Estimate parameters numbers of infections from number of symptom onsets, using a convolution model
