Introduction to statistical concepts used in the course

Nowcasting and forecasting of infectious disease dynamics

Why statistical concepts?

  • We’ll need to estimate things (delays, reproduction numbers, case numbers now and in the future)

  • We’ll want to correctly specify uncertainty

  • We’ll want to incorporate our domain expertise

  • We’ll do this using Bayesian inference

Bayesian inference in 15 minutes

Interlude: probabilities

Laplace, 1812

Probability theory is nothing but common sense reduced to calculation.

Interlude: probabilities (1/3)

  • If \(A\) is a random variable, we write \[ p(A = a)\] for the probability that \(A\) takes value \(a\).
  • We often write \[ p(A = a) = p(a)\]
  • Example: The probability that it rains tomorrow \[ p(\mathrm{tomorrow} = \mathrm{rain}) = p(\mathrm{rain})\]
  • Normalisation \[ \sum_{a} p(a) = 1 \]

Interlude: probabilities (2/3)

  • If \(A\) and \(B\) are random variables, we write \[ p(A = a, B = b) = p(a, b)\] for the joint probability that \(A\) takes value \(a\) and \(B\) takes value \(b\)
  • Example: The probability that it rains today and tomorrow \[ p(\mathrm{tomorrow} = \mathrm{rain}, \mathrm{today} = \mathrm{rain}) = p(\mathrm{rain}, \mathrm{rain})\]
  • We can obtain a marginal probability from joint probabilities by summing \[ p(a) = \sum_{b} p(a, b)\]

Interlude: probabilities (3/3)

  • The conditional probability of getting outcome \(a\) from random variable \(A\), given that the outcome of random variable \(B\) was \(b\), is written as \[ p(A = a | B = b) = p(a| b) \]
  • Example: the probability that it rains tomorrow given that it is sunny today \[ p(\mathrm{tomorrow} = \mathrm{rain} | \mathrm{today} = \mathrm{rain}) = p(\mathrm{rain} | \mathrm{rain})\]
  • Conditional probabilities are related to joint probabilities as \[ p(a | b) = \frac{p(a, b)}{p(b)}\]
  • We can combine conditional probabilities in the chain rule \[ p(a, b, c) = p(a | b, c) p(b | c) p (c) \]

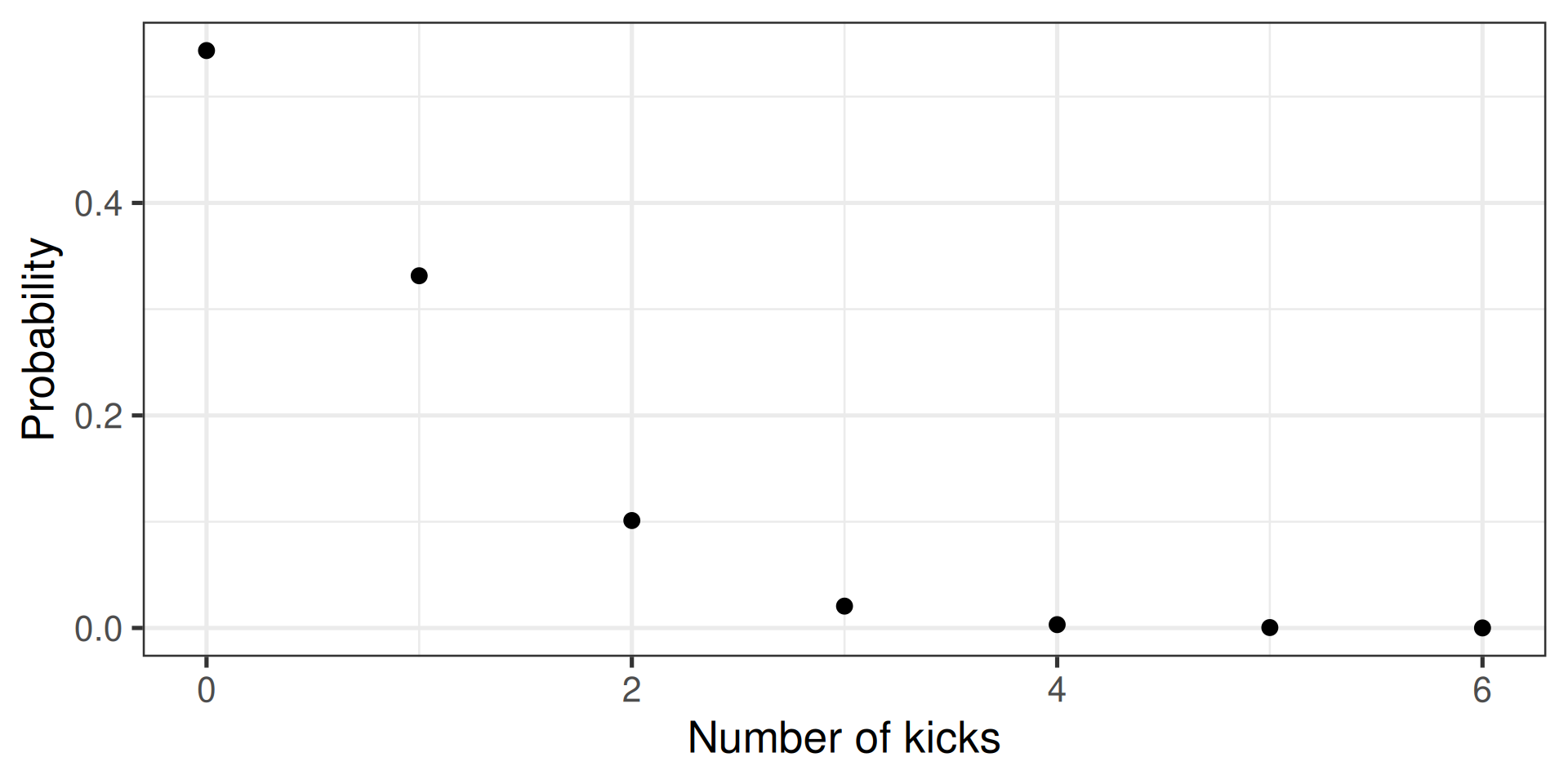
Probability distributions (discrete)

  • E.g., how many people die of horse kicks if there are 0.61 kicks per year
  • Described by the Poisson distribution

Two directions

  1. Calculate the probability
  2. Randomly sample

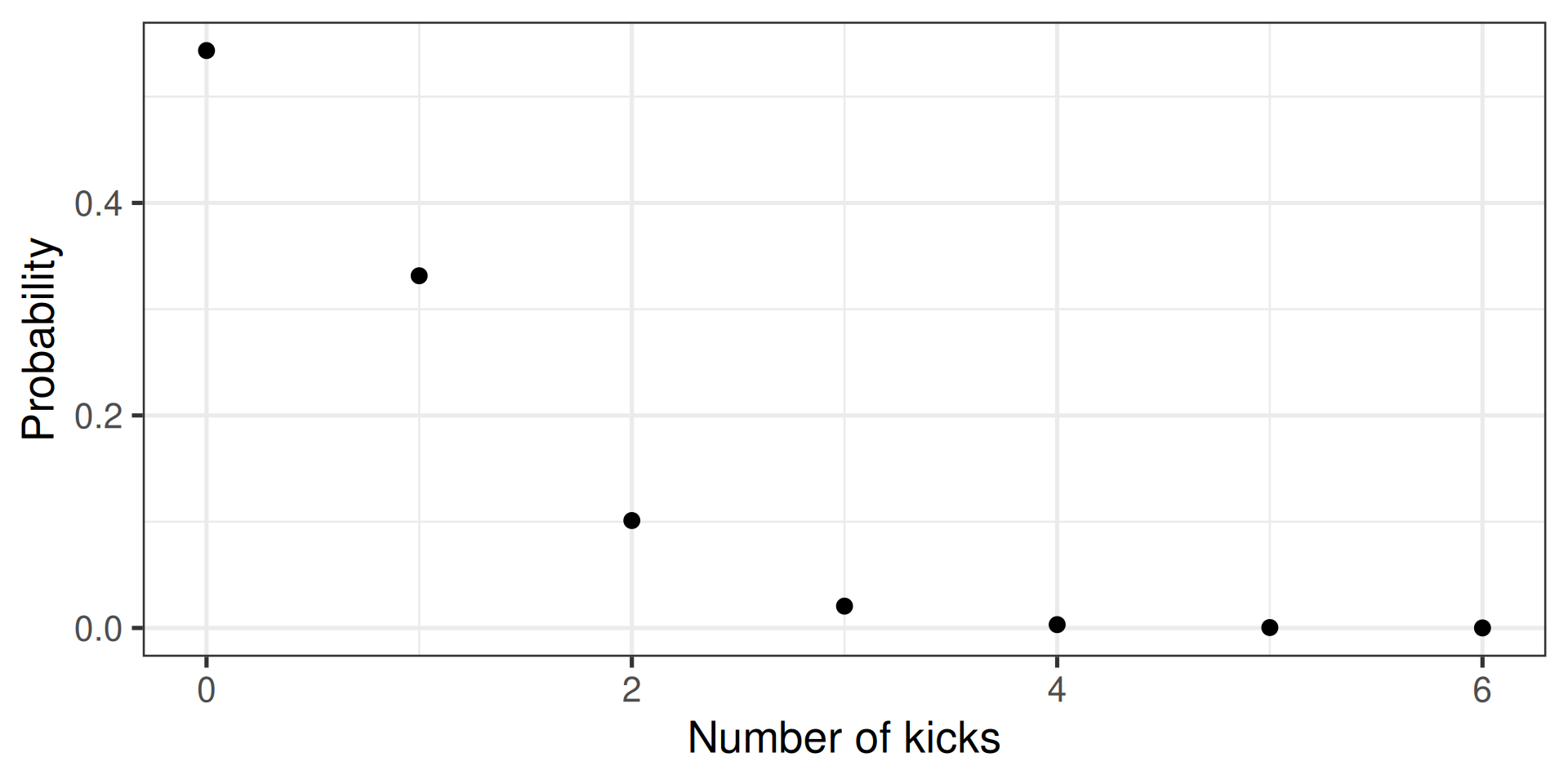
Calculate discrete probability

  • E.g., how many people die of horse kicks if there are 0.61 kicks per year
  • Described by the Poisson distribution

What is the probability of 2 deaths in a year?

  dpois(x = 2, lambda = 0.61)
[1] 0.1010904

Two directions

  1. Calculate the probability
  2. Randomly sample

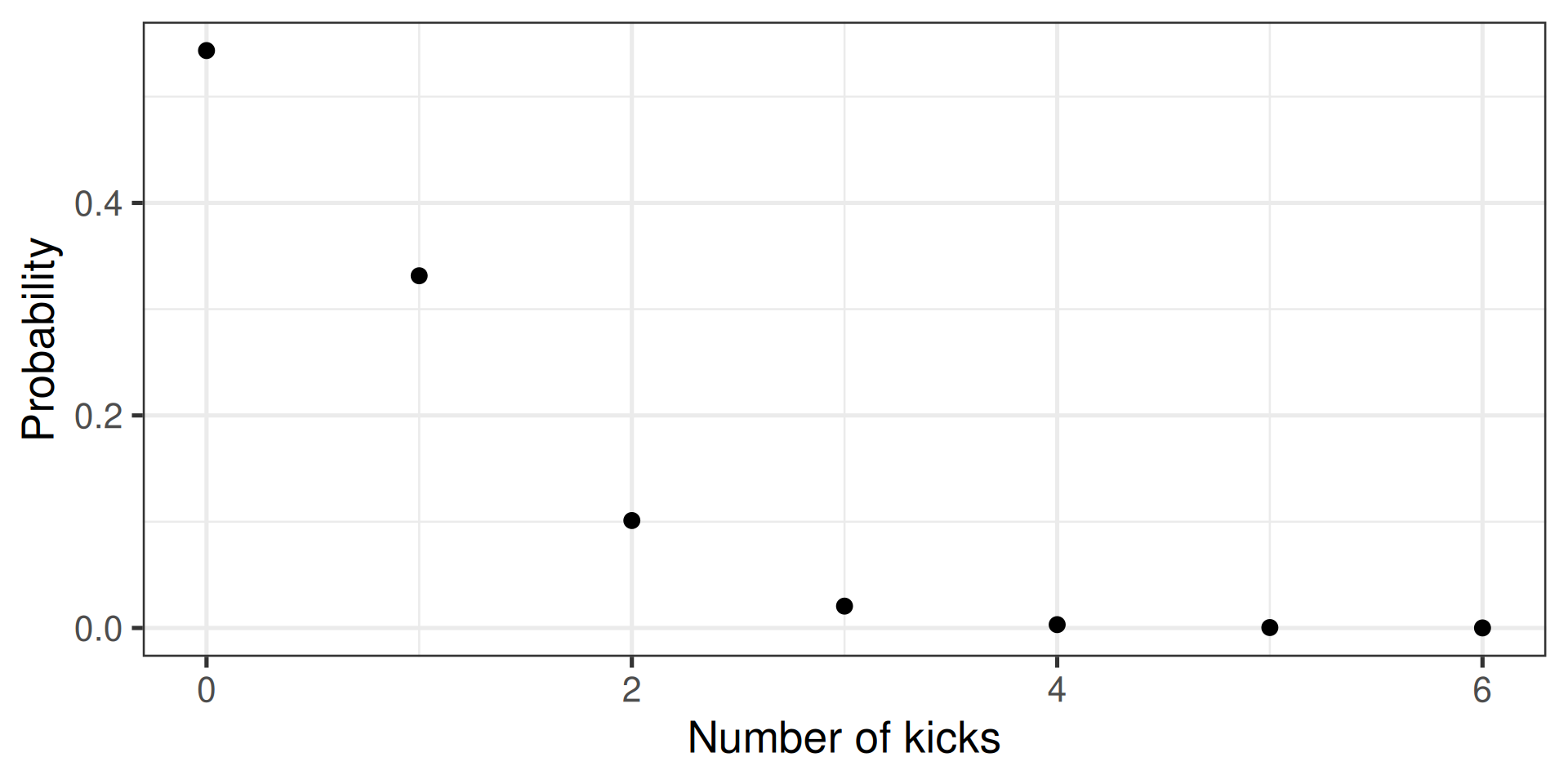
Generate a random (Poisson) sample

  • E.g., how many people die of horse kicks if there are 0.61 kicks per year
  • Described by the Poisson distribution

Generate one random sample from the probability distribution

  rpois(n = 1, lambda = 0.61)
[1] 0

Two directions

  1. Calculate the probability
  2. Randomly sample

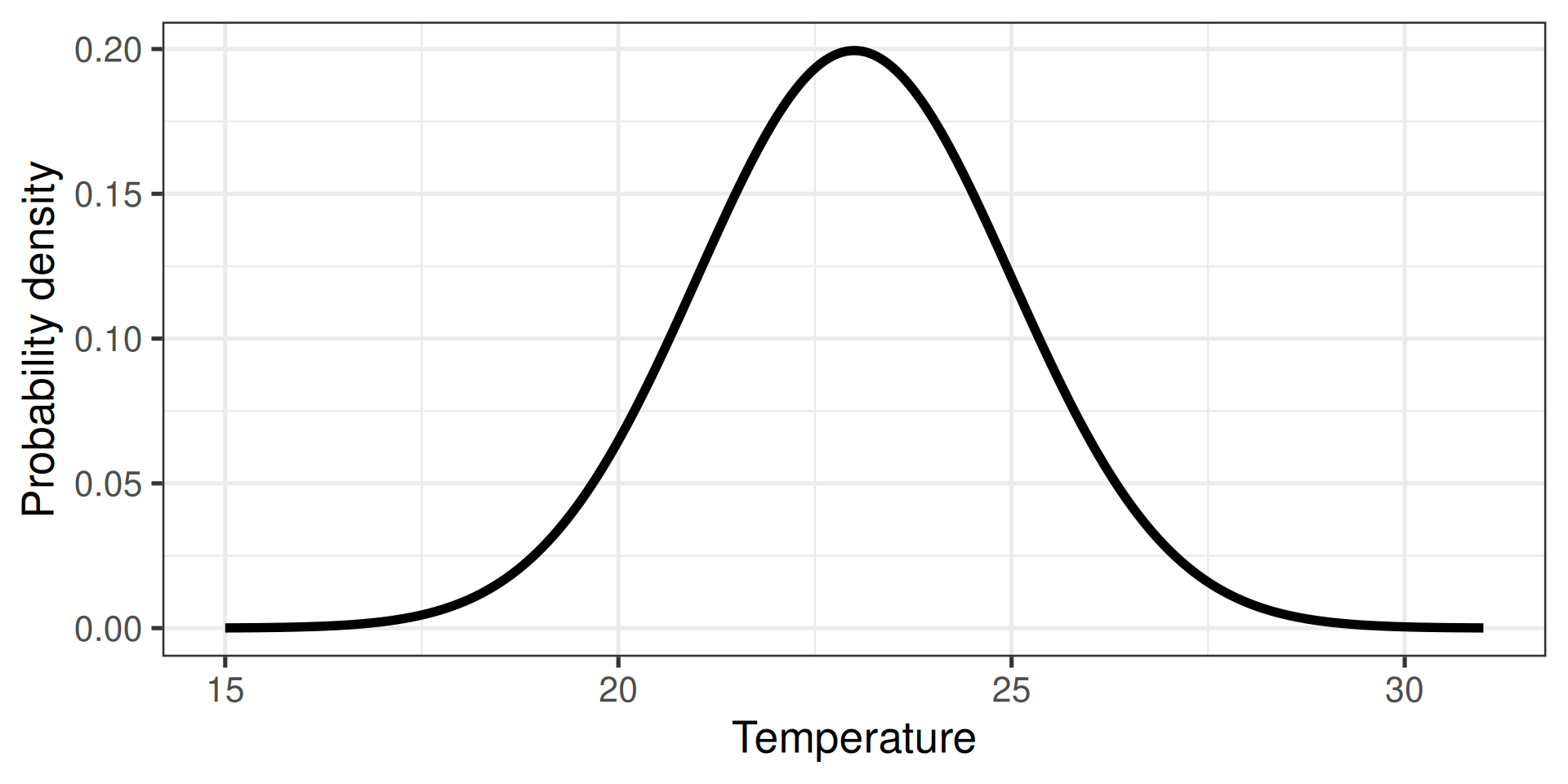
Probability distributions (continuous)

  • Extension of probabilities to continuous variables
  • E.g., the temperature in Stockholm tomorrow

Normalisation: \[ \int p(a) da = 1 \]

Marginal probabilities: \[ p(a) = \int_{} p(a, b) db\]

Two directions

  1. Calculate the probability (density)
  2. Randomly sample

Calculate probability density

  • Extension of probabilities to continuous variables
  • E.g., the temperature in Stockholm tomorrow

What is the probability density of \(30^\circ C\) tomorrow, if the mean temperature on the day is \(23^\circ C\) (standard deviation \(2^\circ C\)) ? A naïve model could be:

  dnorm(x = 30,
        mean = 23,
        sd = 2)
[1] 0.0004363413

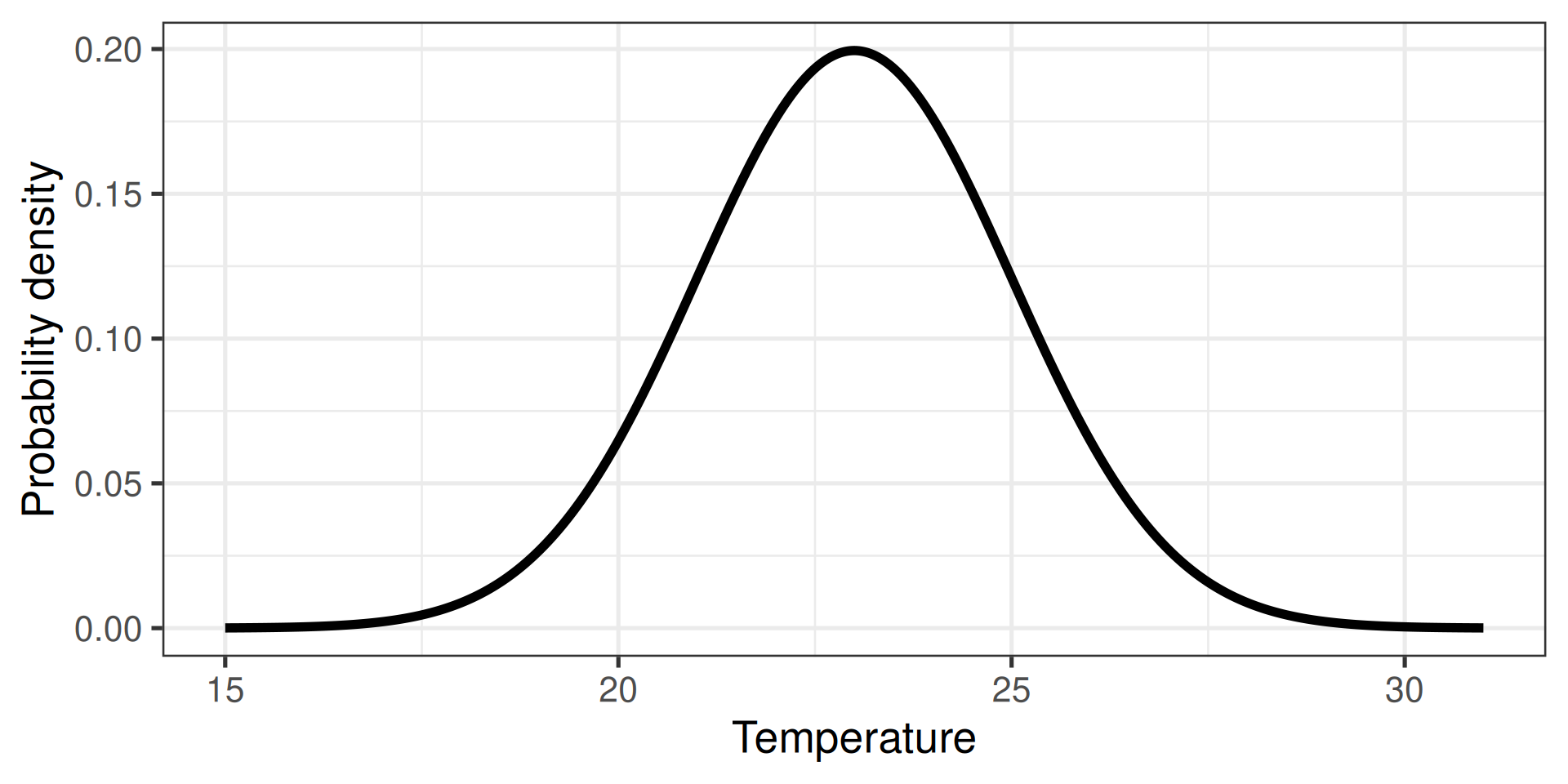
Two directions

  1. Calculate the probability
  2. Randomly sample

Generate a random (normal) sample

Generate one random sample from the normal probability distribution with mean 23 and standard deviation 2:

  rnorm(n = 1,
        mean = 23,
        sd = 2)
[1] 24.60111

Two directions

  1. Calculate the probability
  2. Randomly sample

Bayesian inference in 15 minutes

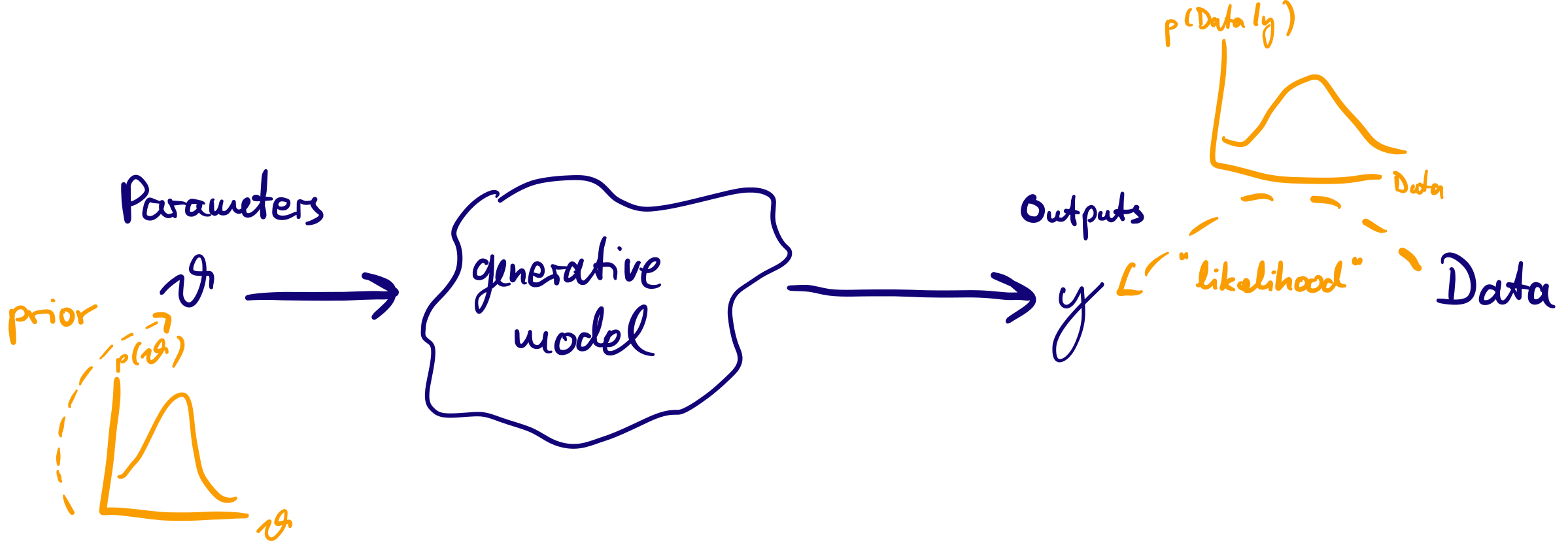
Idea of Bayesian inference: treat \(\theta\) as random variables (with a probability distribution) and condition on data: posterior probability \(p(\theta | \mathrm{data})\) as target of inference.

Bayes’ rule

  • We treat the parameters of the a \(\theta\) as random with prior probabilities given by a distribution \(p(\theta)\). Confronting the model with data we obtain posterior probabilities \(p(\theta | \mathrm{data})\), our target of inference. Applying the rule of conditional probabilities, we can write this as

\[ p(\theta | \textrm{data}) = \frac{p(\textrm{data} | \theta) p(\theta)}{p(\textrm{data})}\]

  • \(p(\textrm{data} | \theta)\) is the /likelihood/

  • \(p(\textrm{data})\) is a /normalisation constant/

  • In words, \[\textrm{(posterior)} \propto \textrm{(normalised likelihood)} \times \textrm{(prior)}\]

Bayesian inference

MCMC

  • Markov-chain Monte Carlo (MCMC) is a method to generate samples from the posterior distribution, the target of inference

  • stan is a probabilistic programming language that helps you to write down probabilistic models and to fit them using MCMC samplers and other methods.

Return to the session

Introduction to statistical concepts used in the course