Nowcasting and forecasting of infectious disease dynamics
Which Model to Use?
There are many types of models available to us, (you’ve already seen a lot now):
A range of choices from mechanistic to purely statistical.
Bayesian, frequentist, machine learning.
Stochastic vs. Deterministic
How should we decide which model(s) to incorporate for nowcasting and forecasting?
What outputs and features do we require of these models?
Using Data to Help Inform your Modeling Choices
Often, what motivates one’s modeling choices are the trends and patterns observed in the data.
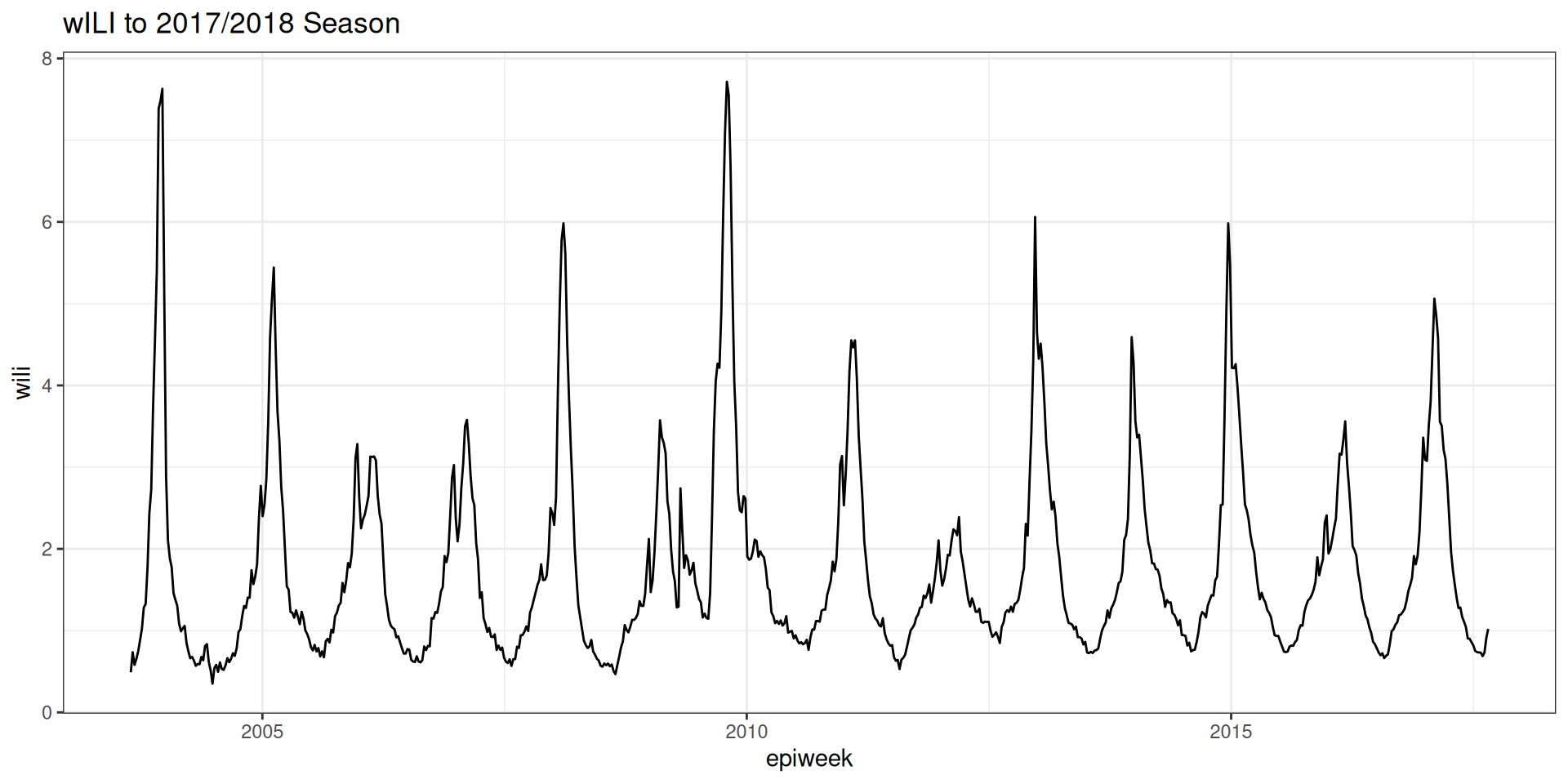
Features we cover in this session
Auto correlation
Partial auto-correlation
Stationarity
Seasonality
Constant variance
Autocorrelation
Autocorrelation and Partial Autocorrelation (ACF/PACF) plots measure the linear relationship between lagged values of a time series.
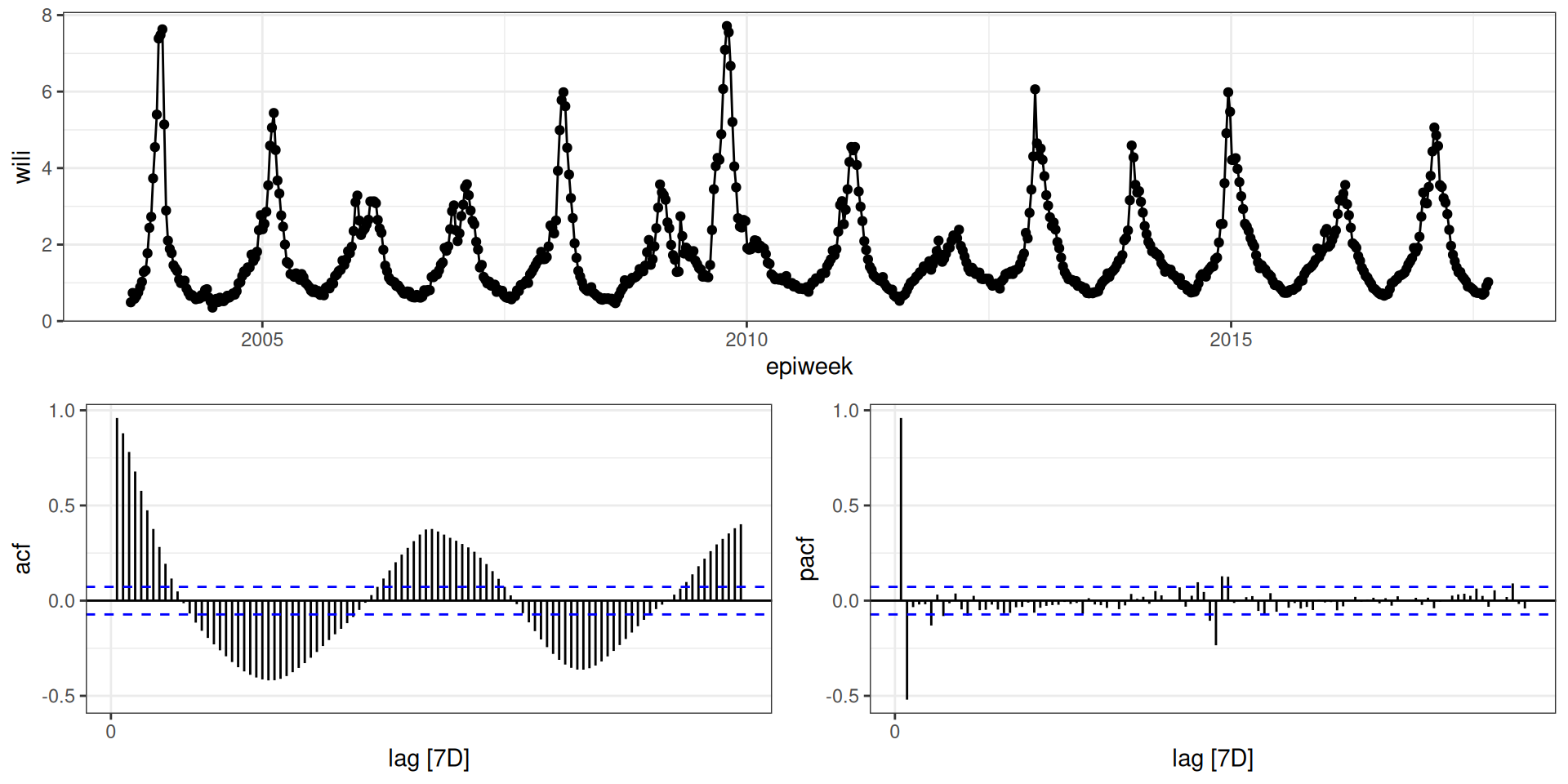
Describing autocorrelation
ACF plots correlation of \(y_t\) and \(y_{t-k}\) as a function of k.
Correlations show periodicity of ~52 weeks.
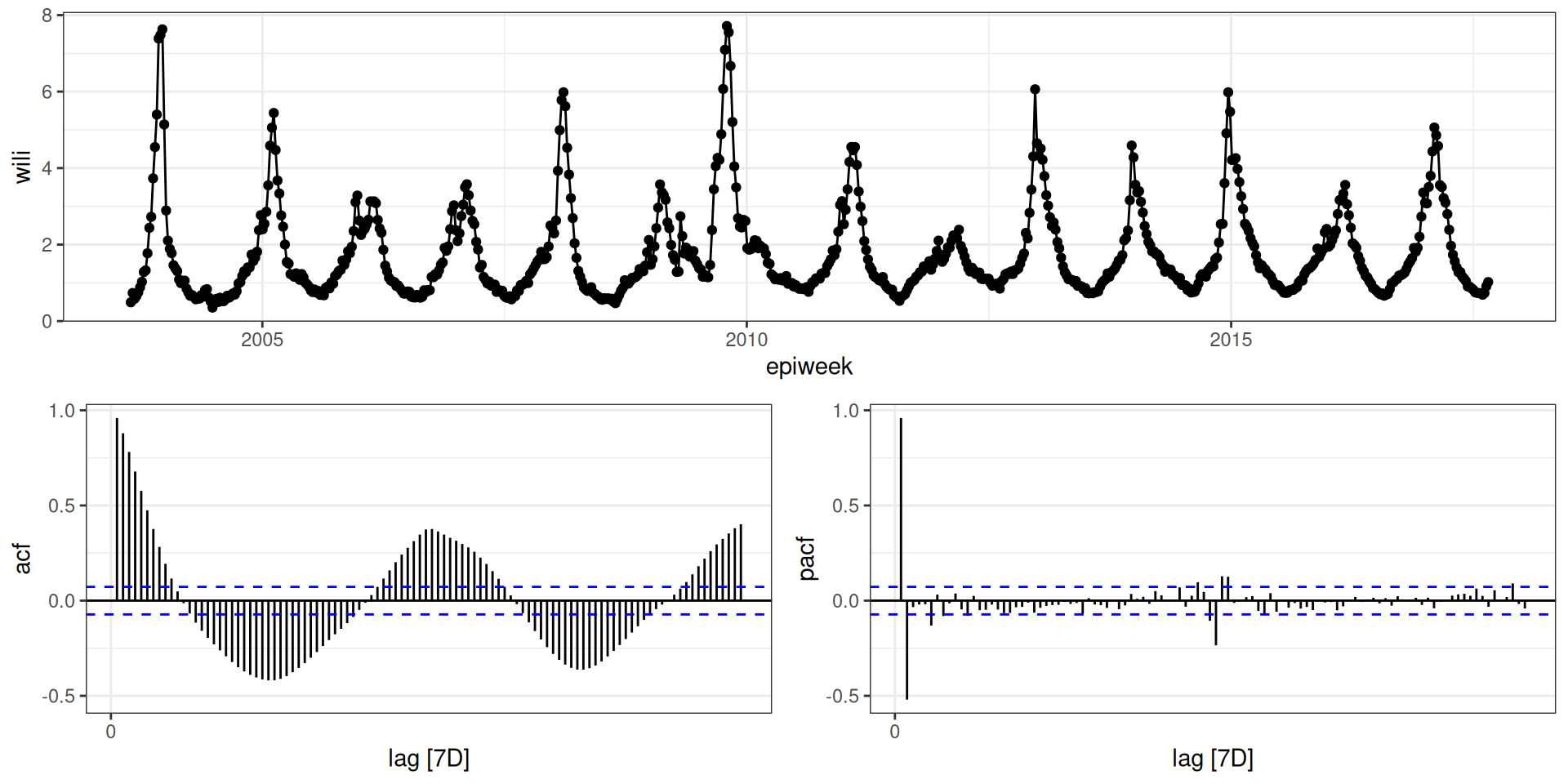
Describing partial correlation
PACF plots correlation of \(y_t\) and \(y_{t-k}\) as a function of k, adjusted for shorter lags.
Only a few partial correlations are significant.
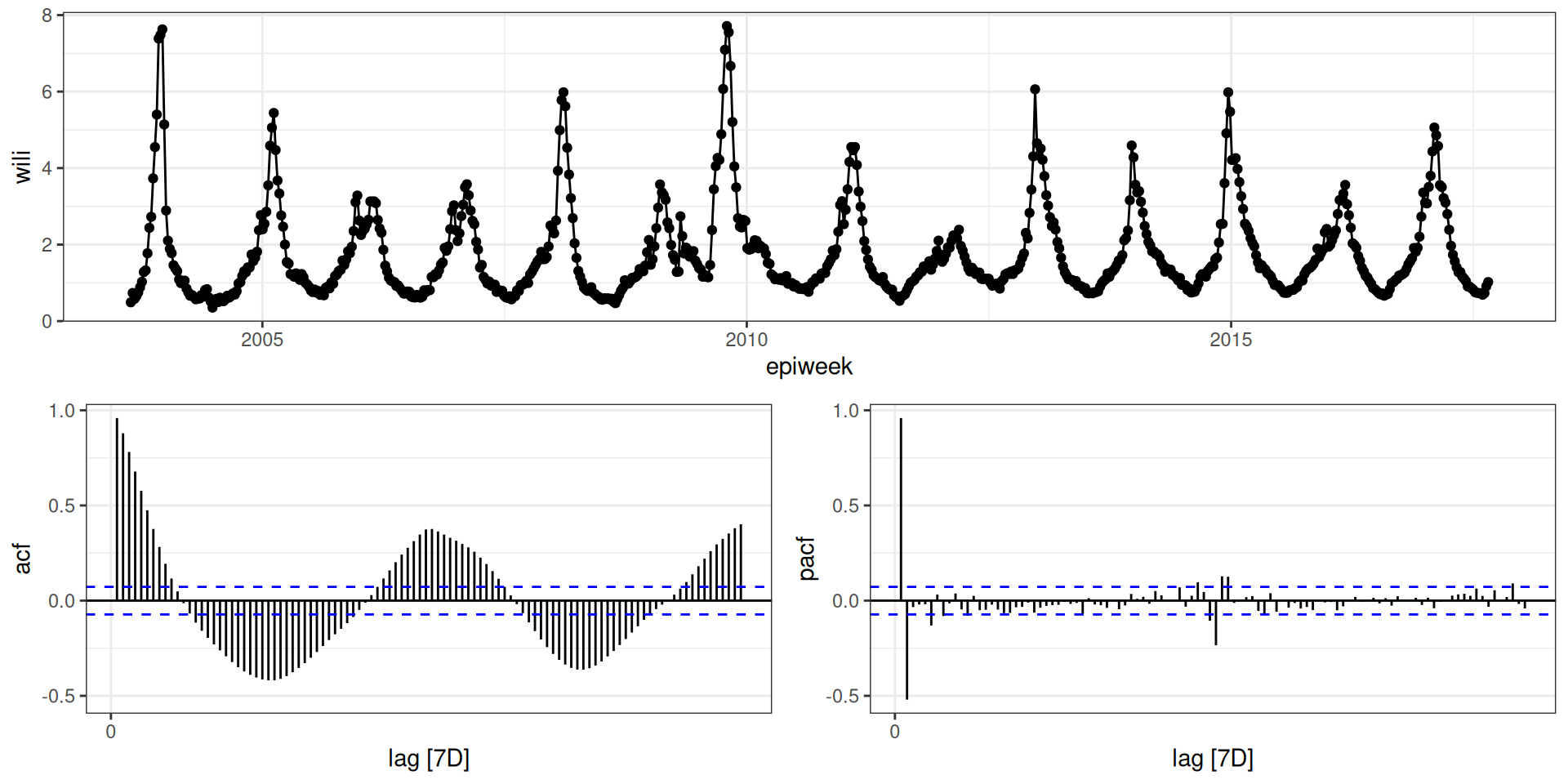
Stationarity
A time series is stationary if the mean and variance of the data do not change over time. Stationarity means that there are no long-term predictable patterns in a time-series, but there can still be predictability in the short term. ARIMA (and other models) assume data are stationary (won’t work as well if data are not).
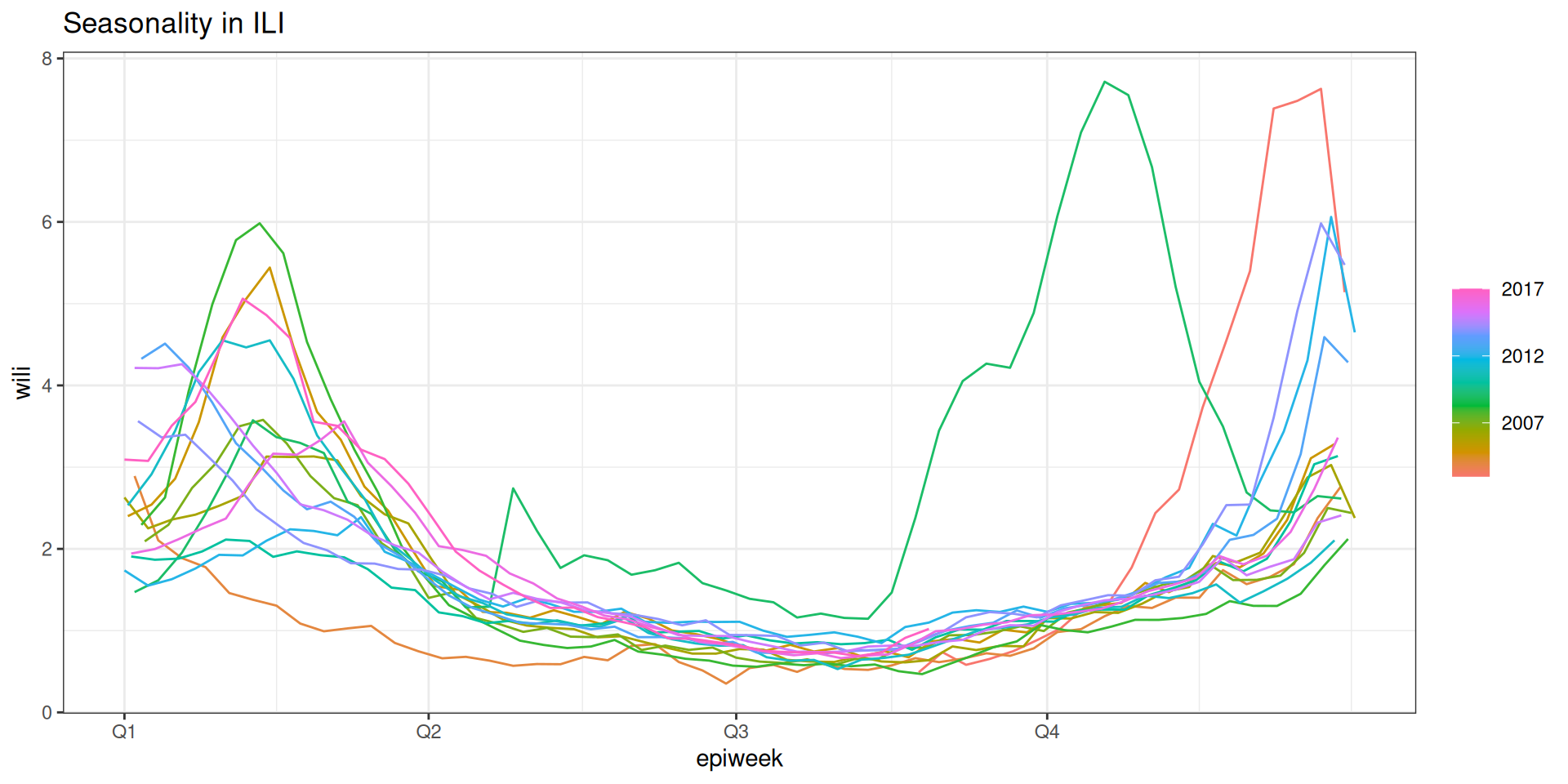
Seasonality
Seasonal patterns are common with many (but not all) endemic diseases. Seasonality can make a disease more predictable, but also means it’s not stationary.
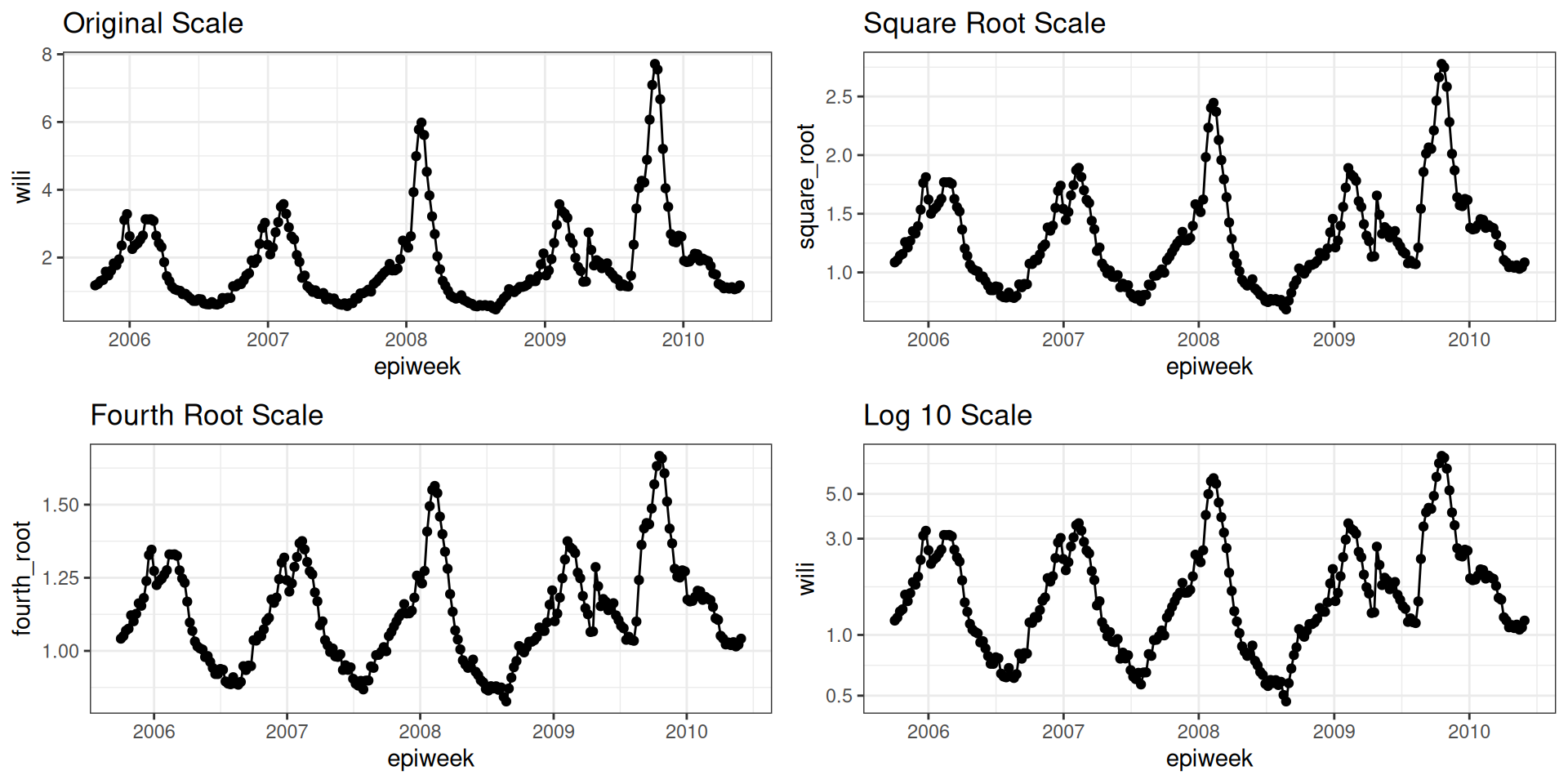
Constant variance
A key assumption of many models is constant variance over time. Transformations often help.
Time-series Regression Models: ARIMA
Widely used for decades!
Notation is \(ARIMA(p, d, q).\)
AR (Auto-Regressive order \(p\))
Uses past values to predict current ones.
Useful when there is auto-correlation.
I (Integrated order \(d\))
Differences (\(y_t - y_{t-1}\)) help make the series stationary.
Useful when there is non-stationarity.
MA (Moving Average order \(q\))
Uses recent model residuals as predictors.
Figuring out which \((p,d,q)\) to use is tricky!
Your Turn
Explore the influenza dataset, focusing on assessing observed patterns qualitatively and quantitatively.
Explore different ways of improving modeling forecasts by incorporating patterns observed in data into our models.
