Combining nowcasting and forecasting
Nowcasting and forecasting of infectious disease dynamics
Motivating example
Often we want to forecast from data like this
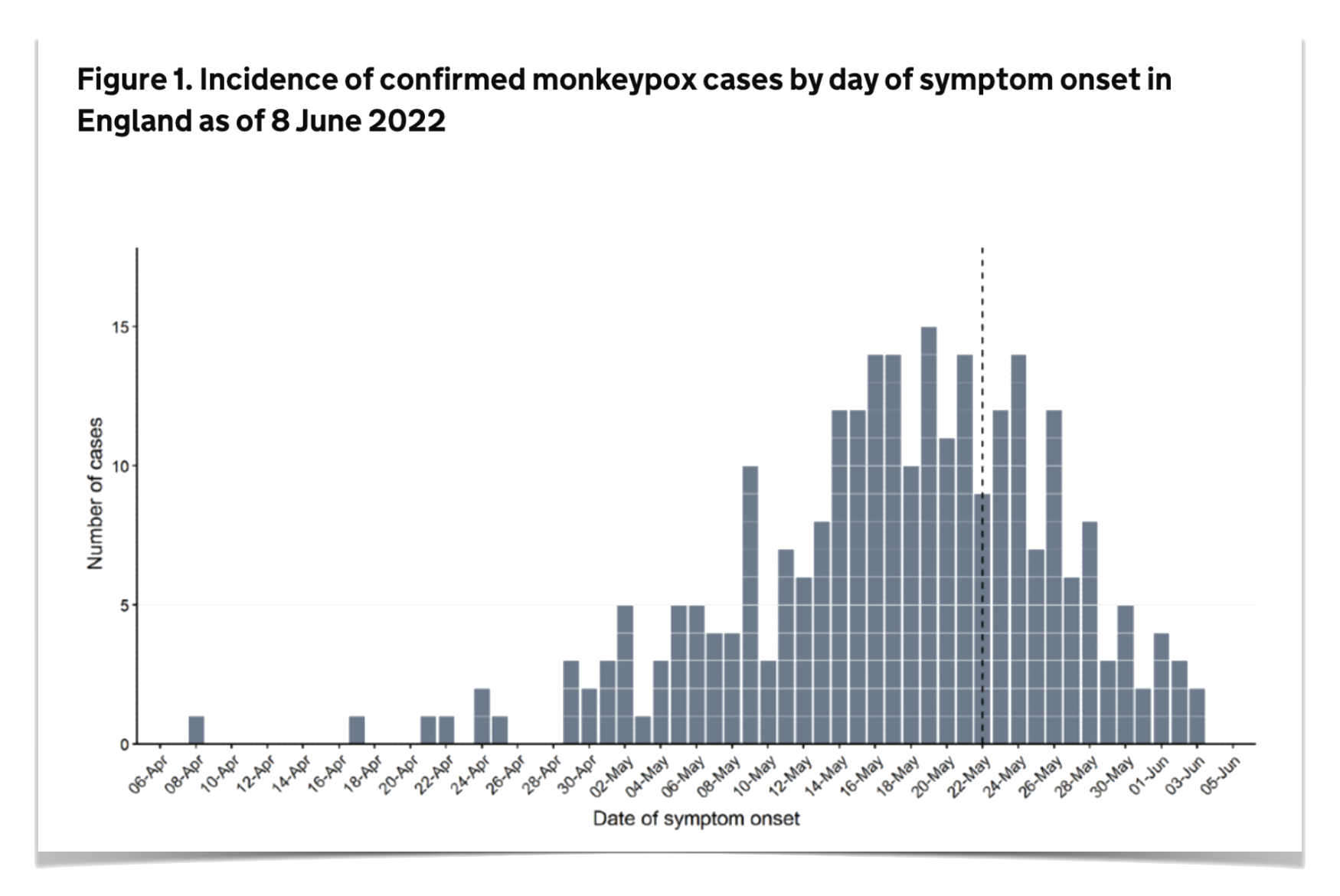
Data after the dashed line are marked as uncertain. How can we use them for forecasting?
The problem: Forecasting with incomplete data
Traditional approach: Wait for “complete” data
- Might mean forecasting from 2+ weeks ago
- But as we’ve seen, forecasts after 2 weeks can be difficult
- Even our forecasts of “what is happening now” end up quite uncertain
The challenge:
- Reporting delays mean recent data are incomplete
- But we need forecasts based on the most recent information
- How do we bridge this gap?
Nowcasting reminder
Predict what an epidemiological time series will look like after all delayed reports are in.
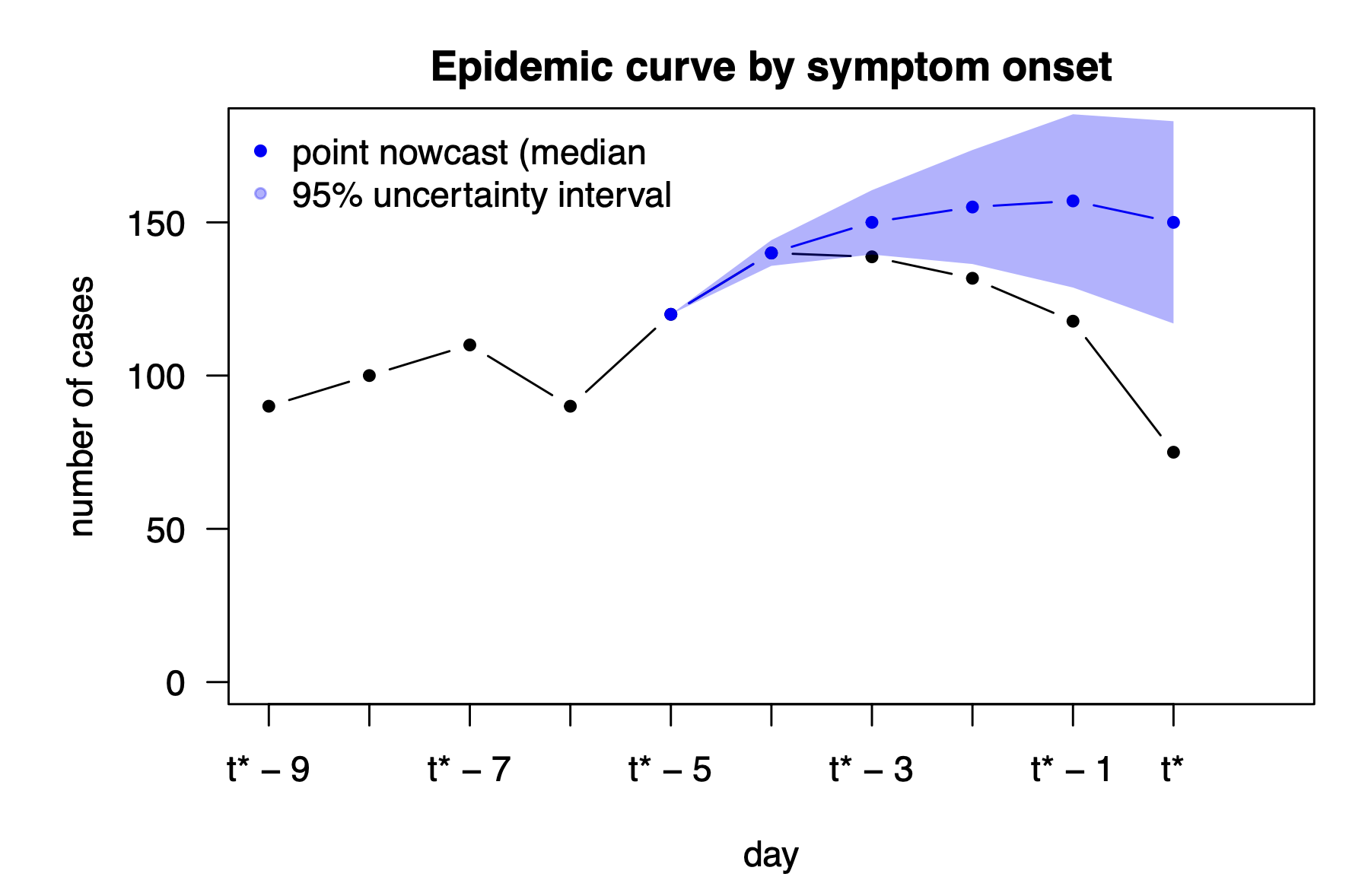
(slide courtesy of Johannes Bracher)
The nowcasting-forecasting continuum
Key insight: Nowcasting and forecasting aren’t distinct
- As we saw in the renewal session, even nowcasting \(R_t\) in real-time is partly a forecast
- Really we have a continuum of more or less information
- Some methods (e.g., Bayesian generative models) make this connection clear
- Others require more thought about how to link them
Approach 1: Complete data approach
- Filter to “complete” data only
- Standard forecast from truncated series
- Problem: Throws away recent information
Approach 2: Pipeline approach (point estimates)
- Point estimate correction for truncation
- Forecast from “adjusted” data
- Problem: No uncertainty propagation
Approach 3: Pipeline approach (with uncertainty)
- Sample from nowcast posterior
- Forecast from multiple trajectories
- Better: Some uncertainty propagation
- But: Still treating nowcast and forecast as separate steps
Approach 4: Joint approach
- Simultaneous nowcast and forecast
- Full Bayesian inference
- Advantage: Proper uncertainty quantification
- Trade-off: More complex to implement
Questions to consider
For each approach:
- How much data does it use?
- Where does uncertainty come from?
- What assumptions are we making?
- When might it work well or poorly?
Your Turn
- Generate example data with realistic truncation
- Implement 4 forecasting approaches (complete data, pipeline, joint)
- Compare performance quantitatively
- Discuss trade-offs and applications
Combining nowcasting and forecasting