Combining nowcasting and forecasting

Introduction

In the previous sessions, we’ve explored nowcasting (estimating what current data will look like once all reports are in) and forecasting (predicting future trends) as separate problems. However, in real-time epidemic analysis, these challenges are connected. When we want to forecast from the most recent data, we face the problem that this data is incomplete due to reporting delays.

In this session, we’ll explore different approaches to handling this challenge, from simple methods that ignore the problem to joint models.

Slides

Combining nowcasting and forecasting

Objectives

This session aims to show how to combine nowcasting and forecasting to make better predictions when data are subject to reporting delays.

Setup

Source file

The source file of this session is located at sessions/forecasting-nowcasting.qmd.

Libraries used

In this session we will use the nfidd package to load a data set of infection times and access Stan models and helper functions, the dplyr and tidyr packages for data wrangling, ggplot2 library for plotting, the tidybayes package for extracting results of the inference, and scoringutils for forecast evaluation.

library("nfidd")
library("dplyr")
library("tidyr")
library("ggplot2")
library("tidybayes")
library("scoringutils")

Tip

The best way to interact with the material is via the Visual Editor of RStudio.

Initialisation

We set a random seed for reproducibility. Setting this ensures that you should get exactly the same results on your computer as we do. We also set an option that makes cmdstanr show line numbers when printing model code. This is not strictly necessary but will help us talk about the models. Finally, we set an option to not warn about the partial definition of initial conditions.

set.seed(123)
options(cmdstanr_print_line_numbers = TRUE)
options(cmdstanr_warn_inits = FALSE)

The challenge: forecasting with incomplete data

As we’ve seen in previous sessions, epidemiological data often arrives with delays. When we want to forecast future trends, we ideally want to use the most recent data available. However, this recent data is incomplete due to reporting delays.

The traditional approach is to wait until data is “complete” (or nearly so) before forecasting. But this might mean forecasting from data that is several weeks old (though more often a few days for most reporting to be complete). As we’ve seen, forecasts degrade quickly with longer forecast horizons, so even our forecasts of “what is happening now” might end up being quite uncertain.

The nowcasting-forecasting continuum

As we discussed in the renewal equation session, even nowcasting \(R_t\) in real-time is partly a forecast for recent time points due to delays from infection to the reporting of data. Nowcasting and forecasting aren’t distinct activities - they exist on a continuum:

Nowcasting: We have some data from the dates we’re predicting
Forecasting: We have no data from the dates we’re predicting

Some methods (particularly Bayesian generative models) make this connection explicit, while others require more thought about how to link these two tasks.

Simulating data for our analysis

We’ll start by generating synthetic data that mimics the challenges we face in real-time epidemic analysis. This builds on the approach from the joint nowcasting session, but now we’ll also create a dataset filtered at a two-week forecast horizon for evaluation (i.e. the data that we would ultimately observe for the two weeks after the forecast date).

Connecting to ILI forecasting

While we use the linelist data (individual symptom onsets with reporting delays) for clarity in this session, the forecasting sessions focus on ILI percentage data. These data types differ substantially:

Our simulated data:

Individual events with systematic reporting delays
Delays cause under-reporting that resolves over time
Clear temporal progression: infection → onset → report

ILI surveillance data (from forecasting sessions):

Compound measure: % of visits for influenza-like illness
Can be revised up OR down as reports arrive
Combines multiple diseases and reporting locations

Adapting these methods for ILI:

The joint modelling framework can handle bidirectional revisions by modelling the full revision process with minor modifications
Pipeline approaches may need separate models for upward and downward revisions
Understanding the data generation process (how individual reports → ILI %) helps identify biases
Performance may be limited by the complexity of the compound measure

The key insight is that whether dealing with simple delays or complex revisions, combining nowcasting and forecasting in a coherent framework improves predictions.

One approach that has been taken in previous work is to use the number of hospitals that have reported in order to estimate how much reporting revisions to expect. These data are actually available in the data we downloaded from epidatar earlier in the course.

Generate the underlying epidemic

First, let’s generate our simulated onset dataset as we did in previous sessions:

gen_time_pmf <- make_gen_time_pmf()
ip_pmf <- make_ip_pmf()
onset_df <- simulate_onsets(
  make_daily_infections(infection_times), gen_time_pmf, ip_pmf
)
head(onset_df)

# A tibble: 6 × 3
    day onsets infections
  <dbl>  <int>      <int>
1     1      0          0
2     2      0          1
3     3      0          0
4     4      1          2
5     5      0          1
6     6      0          1

# Set our analysis cutoff point
cutoff <- 61
forecast_horizon <- 14  # We'll forecast 14 days ahead

Apply reporting delays

Now we’ll simulate reporting delays and create our reporting triangle:

reporting_delay_pmf <- censored_delay_pmf(
  rlnorm, max = 15, meanlog = 1, sdlog = 0.5
)
plot(reporting_delay_pmf)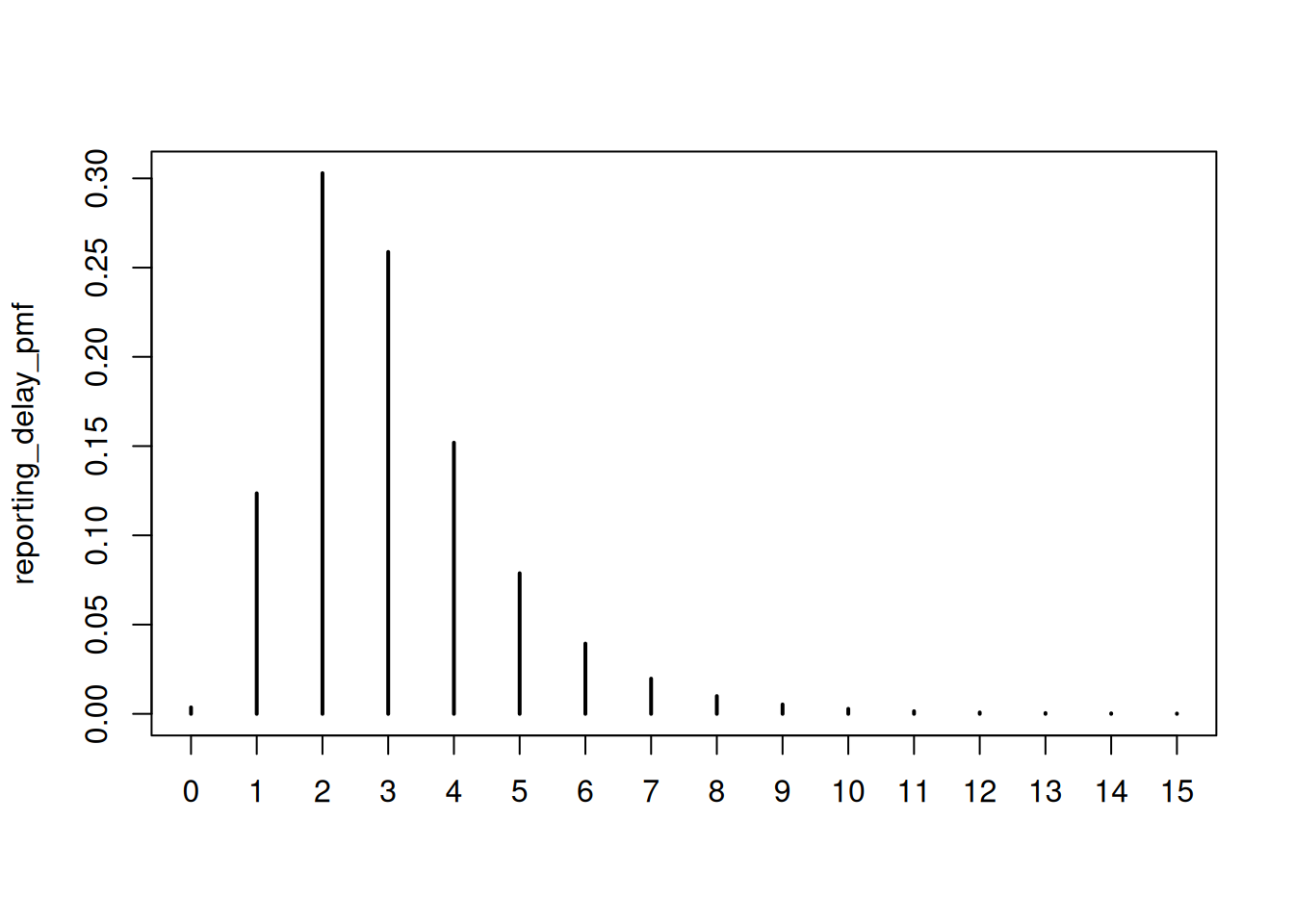

reporting_triangle <- onset_df |>
  filter(day <= cutoff + forecast_horizon) |>
  mutate(
    reporting_delay = list(
      tibble(d = 0:15, reporting_delay = reporting_delay_pmf)
    )
  ) |>
  unnest(reporting_delay) |>
  mutate(
    reported_onsets = rpois(n(), onsets * reporting_delay)
  ) |>
  mutate(reported_day = day + d)

# Filter to what would be observed by the cutoff
filtered_reporting_triangle <- reporting_triangle |>
  filter(reported_day <= cutoff)

tail(filtered_reporting_triangle)

# A tibble: 6 × 7
    day onsets infections     d reporting_delay reported_onsets reported_day
  <dbl>  <int>      <int> <int> <table[1d]>               <int>        <dbl>
1    59     37         59     0 0.00363684                    0           59
2    59     37         59     1 0.12356754                    4           60
3    59     37         59     2 0.30290897                    8           61
4    60     43         79     0 0.00363684                    0           60
5    60     43         79     1 0.12356754                    8           61
6    61     45         71     0 0.00363684                    0           61

Now we create the available onsets by summing reported onsets by day - this represents what we observe at the cutoff:

available_onsets <- filtered_reporting_triangle |>
  summarise(available_onsets = sum(reported_onsets), .by = day)

tail(available_onsets)

# A tibble: 6 × 2
    day available_onsets
  <dbl>            <int>
1    56               33
2    57               32
3    58               21
4    59               12
5    60                8
6    61                0

Create forecast evaluation datasets

For our analysis, we need two additional datasets:

Complete data at forecast horizon: What we would observe up to the forecast horizon
Filtered data for complete data approach: Data that is “complete” (i.e. expected to be fully reported) at the time of forecast

# Dataset 1: What we observe over the forecast horizon
complete_at_horizon <- reporting_triangle |>
  filter(day <= cutoff + forecast_horizon) |>
  summarise(complete_onsets = sum(reported_onsets), .by = day)

# Dataset 2: "Complete" data for complete data approach (e.g., >14 days old)
complete_threshold <- 14
complete_data <- available_onsets |>
  filter(day <= cutoff - complete_threshold)

Choosing the “complete data” threshold

We’ve chosen 14 days as our threshold for “complete” data, but this is quite conservative. Let’s examine what proportion of reports we expect to have received by different delays:

# Calculate cumulative reporting proportions
reporting_cdf <- cumsum(reporting_delay_pmf)
tibble(
  delay = 0:15,
  pmf = reporting_delay_pmf,
  cdf = reporting_cdf
) |>
  filter(delay %in% c(1, 3, 5, 7, 10, 14)) |>
  mutate(
    `Proportion reported` = round(cdf, 3),
    `Proportion missing` = round(1 - cdf, 3)
  ) |>
  select(
    `Days since onset` = delay,
    `Proportion reported`,
    `Proportion missing`
  ) |>
  knitr::kable(caption = "Expected reporting completeness by delay")

Expected reporting completeness by delay
Days since onset	Proportion reported	Proportion missing
1	0.127	0.873
3	0.689	0.311
5	0.920	0.080
7	0.979	0.021
10	0.997	0.003
14	1.000	0.000

As we can see, after 5 days we expect to have received ~92% of reports, and after 7 days ~98%. Using a 14-day threshold means we’re losing 7-9 days of potentially useful data.

Trade-offs to consider:

Less conservative thresholds (e.g., 5-7 days): Use more recent data but need to account for 5-15% missing reports
More conservative thresholds (e.g., 14 days): Very complete data but lose recent epidemic trends
Nowcasting approaches: Use all available data and explicitly model the reporting process

Try experimenting with different thresholds (e.g., complete_threshold <- 7) to see how it affects the forecasts!

Now lets visualise the different datasets

ggplot() +
  geom_line(data = complete_at_horizon, 
            aes(x = day, y = complete_onsets, colour = "Complete data"), 
            linewidth = 1) +
  geom_line(data = available_onsets, 
            aes(x = day, y = available_onsets, colour = "Available now"), 
            linewidth = 1) +
  geom_line(data = complete_data, 
            aes(x = day, y = available_onsets, colour = "Complete as of now"), 
            linewidth = 1.2) +
  geom_vline(xintercept = cutoff, linetype = "dotted") +
  geom_vline(xintercept = cutoff - complete_threshold, 
             linetype = "dotted", alpha = 0.5) +
  scale_colour_manual(
    values = c(
      "Complete data" = "black",
      "Available now" = "red", 
      "Complete as of now" = "green"
    )
  ) +
  labs(
    x = "Day",
    y = "Onsets",
    title = "Different views of the data",
    colour = "Data type"
  ) +
  guides(
    colour = guide_legend(nrow = 2)) +
  theme_minimal() +
  theme(legend.position = "bottom")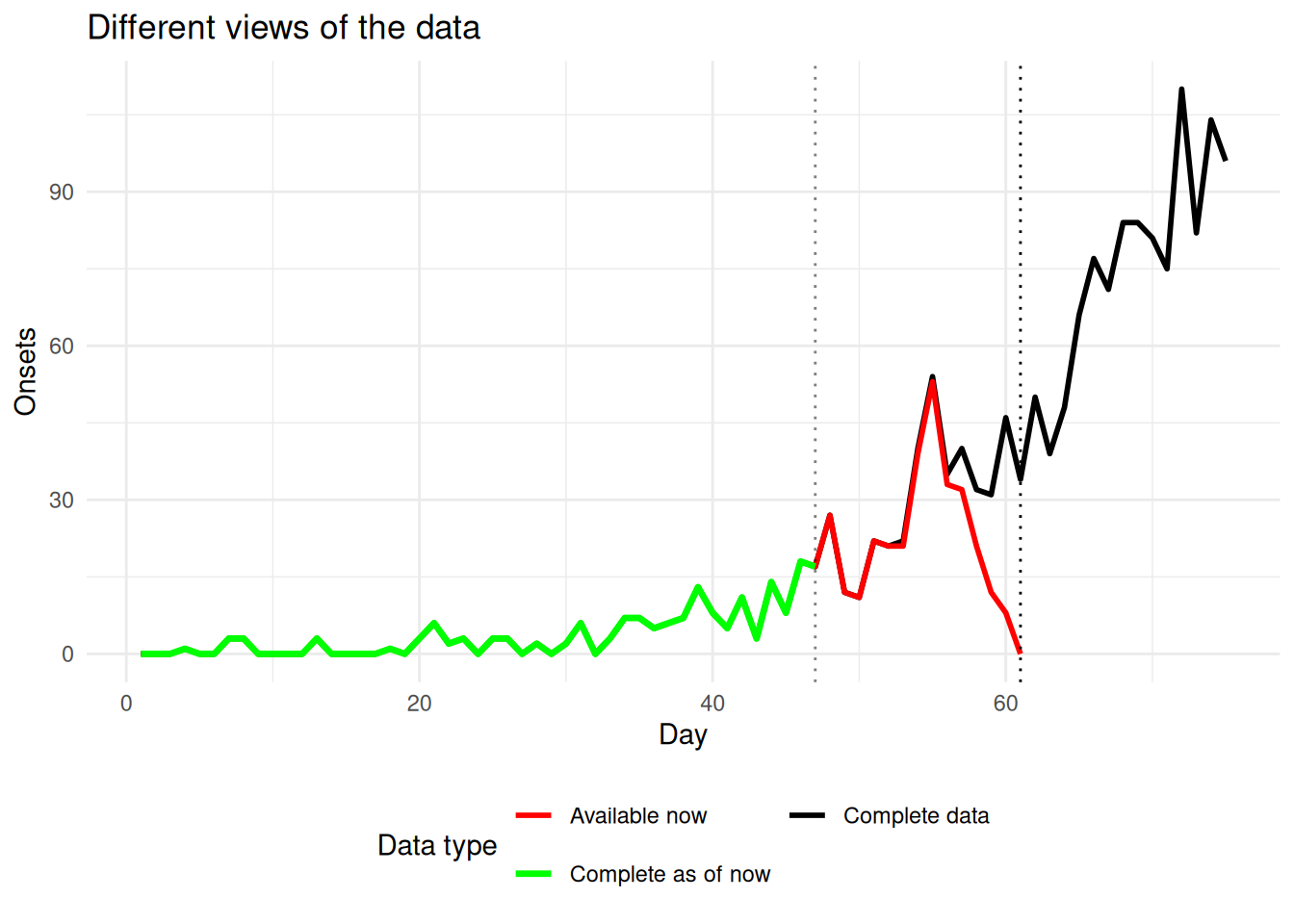

Approach 1: Complete data approach

The simplest approach is to filter to only “complete” data and forecast from there using the renewal model from the reproduction number session. We pick the renewal model as its generative process is consistent with the data we have (i.e. an outbreak). This throws away recent information but avoids the bias from right truncation.

We first load the renewal forecasting model:

renewal_model <- nfidd_cmdstan_model("estimate-inf-and-r-rw-forecast")
renewal_model

 1: functions {
 2:   #include "functions/convolve_with_delay.stan"
 3:   #include "functions/renewal.stan"
 4:   #include "functions/geometric_random_walk.stan"
 5: }
 6: 
 7: data {
 8:   int n;                // number of days
 9:   int I0;              // number initially infected
10:   array[n] int obs;     // observed symptom onsets
11:   int gen_time_max;     // maximum generation time
12:   array[gen_time_max] real gen_time_pmf;  // pmf of generation time distribution
13:   int<lower = 1> ip_max; // max incubation period
14:   array[ip_max + 1] real ip_pmf;
15:   int h;                // number of days to forecast
16: }
17: 
18: parameters {
19:   real<lower = 0> init_R;         // initial reproduction number
20:   array[n-1] real rw_noise; // random walk noise
21:   real<lower = 0, upper = 1> rw_sd; // random walk standard deviation
22: }
23: 
24: transformed parameters {
25:   array[n] real R = geometric_random_walk(init_R, rw_noise, rw_sd);
26:   array[n] real infections = renewal(I0, R, gen_time_pmf);
27:   array[n] real onsets = convolve_with_delay(infections, ip_pmf);
28: }
29: 
30: model {
31:   // priors
32:   init_R ~ normal(1, 0.5) T[0, ];
33:   rw_noise ~ std_normal();
34:   rw_sd ~ normal(0, 0.05) T[0,];
35:   obs ~ poisson(onsets[1:n]);
36: }
37: generated quantities {
38:   array[h] real forecast;
39:   if (h > 0) {
40:     array[n + h - 1] real f_rw_noise;
41:     for (i in 1:(n-1)) {
42:       f_rw_noise[i] = rw_noise[i];
43:     }
44:     for (i in n:(n + h - 1)) {
45:       f_rw_noise[i] = normal_rng(0, 1);
46:     }
47:     array[h + n] real f_R = geometric_random_walk(init_R, f_rw_noise, rw_sd);
48:     array[h + n] real f_infections = renewal(I0, f_R, gen_time_pmf);
49:     array[h + n] real f_onsets = convolve_with_delay(f_infections, ip_pmf);
50:     for (i in 1:h) {
51:       forecast[i] = poisson_rng(f_onsets[n + i]);
52:     }
53:   }
54: }

Reminder

These models are optimised for readability and not robustness or performance. For real-world versions of these models, see the EpiNow2 and epinowcast packages. For the more complex models we might also consider using approximtate fitting methods such as variational inference or integrated nested Laplace approximations.

Take 2 minutes

How does this model differ from the one we used in the Rt estimation session?

Solution

The model is the same as the one we used in the Rt estimation session, but with an additional block where we generate the forecast for additional days beyond the observation period. To do this we need to regenerate the Rt samples for the additional days, and then use these to generate infections and onsets.

Now we fit the model to estimate Rt and forecast:

complete_data_fit <- nfidd_sample(
  renewal_model,
  data = list(
    n = nrow(complete_data),
    I0 = 10,  # Initial number infected
    obs = complete_data$available_onsets,
    gen_time_max = length(gen_time_pmf),
    gen_time_pmf = gen_time_pmf,
    ip_max = length(ip_pmf) - 1,
    ip_pmf = ip_pmf,
    h = forecast_horizon + complete_threshold  # Forecast to beyond cutoff
  ),
  adapt_delta = 0.95,
  max_treedepth = 12,
  init = \() list(init_R = 1, rw_sd = 0.01)  
)

and extract forecast samples for analysis:

complete_data_forecasts <- complete_data_fit |>
  gather_draws(forecast[day], ndraws = 100) |>
  ungroup() |>
  mutate(
    actual_day = day + max(complete_data$day),
    approach = "Complete data"
  )

head(complete_data_forecasts)

# A tibble: 6 × 8
    day .chain .iteration .draw .variable .value actual_day approach     
  <int>  <int>      <int> <int> <chr>      <dbl>      <dbl> <chr>        
1     1      3        486  1486 forecast      14         48 Complete data
2     1      3        136  1136 forecast      19         48 Complete data
3     1      1        165   165 forecast      23         48 Complete data
4     1      1        270   270 forecast       5         48 Complete data
5     1      2        149   649 forecast      18         48 Complete data
6     1      4        491  1991 forecast      14         48 Complete data

Now let’s visualise how this approach performs:

# Plot forecast from forecast date onwards
forecast_start_day <- max(complete_data$day)
evaluation_end_day <- max(complete_at_horizon$day)

ggplot() +
  # Final observed data (truth) for evaluation period
  geom_point(data = complete_at_horizon |> 
               filter(day >= forecast_start_day, day <= evaluation_end_day), 
            aes(x = day, y = complete_onsets), 
            color = "black", size = 1) +
  # Complete data forecast ribbons from forecast start
  geom_line(data = complete_data_forecasts |>
              filter(actual_day >= forecast_start_day, actual_day <= evaluation_end_day),
            aes(x = actual_day, y = .value, group = .draw),
            color = "red", alpha = 0.1) +
  # Mark cutoff date (when we actually want forecasts from)
  geom_vline(xintercept = cutoff, 
             linetype = "dashed", color = "blue", linewidth = 1) +
  scale_y_log10() +
  xlim(forecast_start_day, evaluation_end_day) +
  labs(
    x = "Day",
    y = "Onsets",
    title = "Complete data approach",
    subtitle = "Blue line: Forecast date"
  ) +
  theme_minimal()

Warning in scale_y_log10(): log-10 transformation introduced infinite values.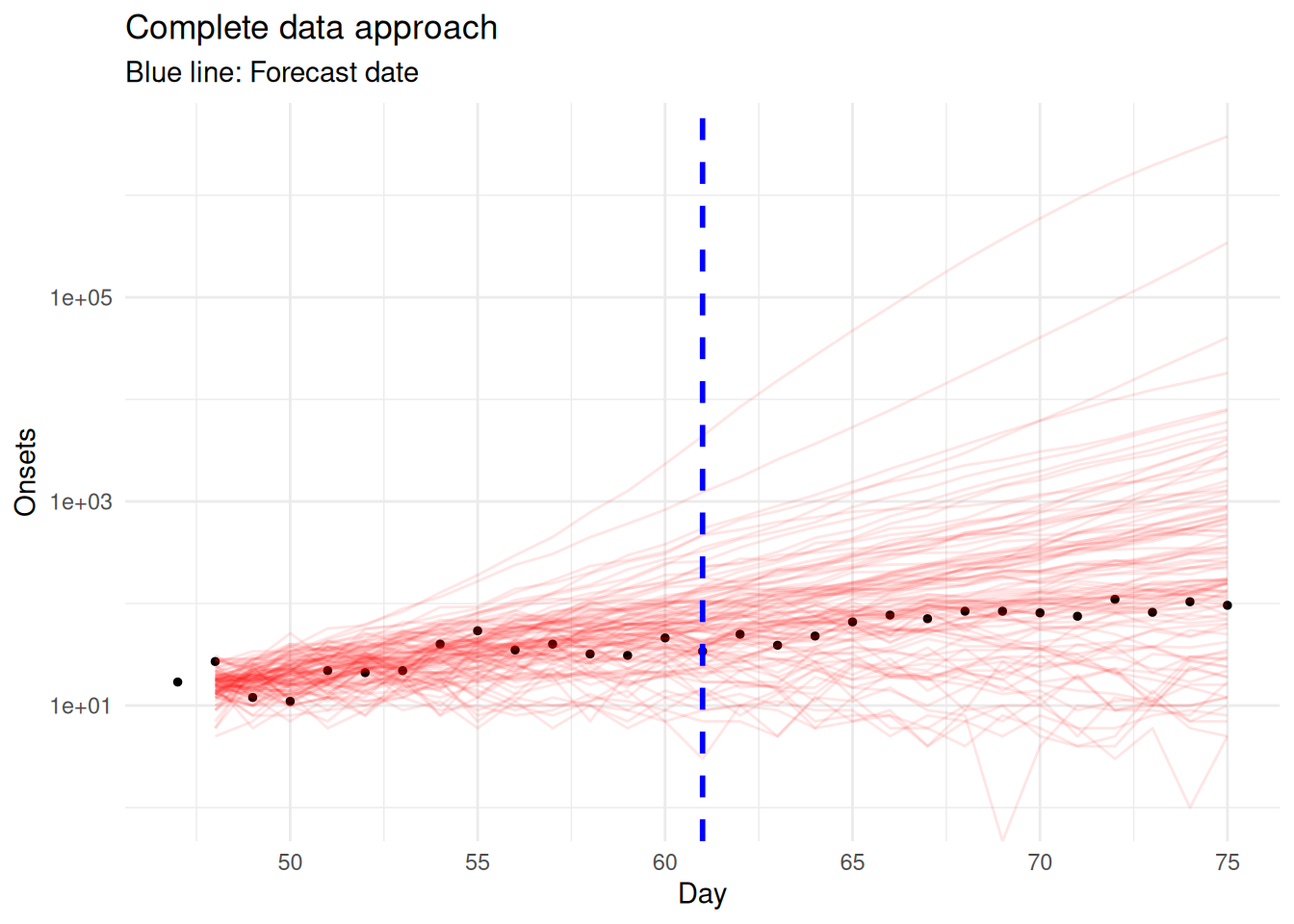

Take 5 minutes

Examine the complete data approach:

How far back does the forecast have to start from?
What happens to forecast uncertainty over the forecast horizon?
Why might this approach miss recent changes in transmission?
What key assumption does this make about data completeness?

Solution

Forecast starts 14 days before cutoff: The approach has to start forecasting from day 57 (cutoff - 14) to reach day 71 (cutoff), creating a very longerforecast horizon
Uncertainty grows: Forecasting over 28+ days (14 to reach cutoff + 14 forecast horizon) leads to very wide prediction intervals when using a random walk for \(R_t\)
Misses recent transmission changes: Any changes in \(R_t\) in the recent 14 days are completely ignored, potentially missing important epidemiological trends
Assumes perfect completeness: Assumes data >14 days old is completely reported, which may not be true for all reporting systems

Approach 2: Pipeline approach (point estimates)

Pipeline approaches vs joint models

In this session, we’ll explore different ways to combine nowcasting and forecasting. Building on methods from our earlier sessions, you could construct pipeline approaches using:

Delay distribution estimation: Methods from the biases in delay distributions session to estimate reporting delays from individual-level data
Simple nowcasting: The geometric random walk nowcasting model from the nowcasting concepts session
Multiplicative baseline methods: Simple CDF-based scaling approaches using tools like baselinenowcast
Reproduction number estimation: Methods from the R estimation session applied to the nowcasted data

Each component can be developed and validated independently, making pipeline approaches more modular and sometimes easier to debug. The trade-off is that uncertainty may not propagate correctly between components, and the assumptions of each component may not be consistent with each other.

As we’ll see, joint models that estimate nowcasts and forecasts together can address these limitations, but come with their own challenges in terms of complexity and computational requirements.

We start by fitting a geometric random walk nowcast to the reporting triangle data, as we did in the joint nowcasting session.

First, we load the joint nowcasting model:

geometric_nowcast_model <- nfidd_cmdstan_model("joint-nowcast")
geometric_nowcast_model

 1: functions {
 2:   #include "functions/geometric_random_walk.stan"
 3:   #include "functions/observe_onsets_with_delay.stan"
 4:   #include "functions/combine_obs_with_predicted_obs_rng.stan"
 5: }
 6: 
 7: data {
 8:   int n;                // number of days
 9:   int m;                // number of reports
10:   array[n] int p;       // number of observations per day
11:   array[m] int obs;     // observed symptom onsets
12:   int d;                // number of reporting delays
13: }
14: 
15: transformed data{
16:   array[n] int P = to_int(cumulative_sum(p));
17:   array[n] int D = to_int(cumulative_sum(rep_array(d, n)));
18: }
19: 
20: parameters {
21:   real<lower=0> init_onsets;
22:   array[n-1] real rw_noise;
23:   real<lower=0> rw_sd;
24:   simplex[d] reporting_delay; // reporting delay distribution
25: }
26: 
27: transformed parameters {
28:   array[n] real onsets = geometric_random_walk(init_onsets, rw_noise, rw_sd);
29:   array[m] real onsets_by_report = observe_onsets_with_delay(onsets, reporting_delay, P, p);
30: }
31: 
32: model {
33:   // Prior
34:   init_onsets ~ normal(1, 5) T[0,];
35:   rw_noise ~ std_normal();
36:   rw_sd ~ normal(0, 0.05) T[0,];
37:   reporting_delay ~ dirichlet(rep_vector(1, d));
38:   // Likelihood
39:   obs ~ poisson(onsets_by_report);
40: }
41: 
42: generated quantities {
43:   array[d*n] real complete_onsets_by_report = observe_onsets_with_delay(onsets, reporting_delay, D, rep_array(d, n));
44:   array[n] int nowcast = combine_obs_with_predicted_obs_rng(obs, complete_onsets_by_report, P, p, d, D);
45: }
46:

Now we fit the geometric nowcast to the reporting triangle:

geometric_nowcast_fit <- nfidd_sample(
  geometric_nowcast_model,
  data = list(
    n = length(unique(filtered_reporting_triangle$day)),
    m = nrow(filtered_reporting_triangle),
    p = filtered_reporting_triangle |>
     group_by(day) |>
     filter(d == max(d)) |>
     mutate(d = d + 1) |>
     pull(d),
    obs = filtered_reporting_triangle$reported_onsets,
    d = 16
  )
)

From the nowcast posterior, we extract point estimates (medians) to use in the forecasting step. This loses uncertainty information.

# Extract nowcast point estimates
nowcast_estimates <- geometric_nowcast_fit |>
  gather_draws(nowcast[day]) |>
  median_qi(.value) |>
  select(day, nowcast = .value)

tail(nowcast_estimates)

# A tibble: 6 × 2
    day nowcast
  <int>   <dbl>
1    56      38
2    57      39
3    58      33
4    59      31
5    60      40
6    61      37

Now we use the renewal model to forecast from this point estimate.

Next, we fit the renewal model to our combined dataset:

pipeline_forecast_fit <- nfidd_sample(
  renewal_model,
  data = list(
    n = nrow(nowcast_estimates),
    I0 = 10,  # Initial number infected
    obs = round(nowcast_estimates$nowcast),
    gen_time_max = length(gen_time_pmf),
    gen_time_pmf = gen_time_pmf,
    ip_max = length(ip_pmf) - 1,
    ip_pmf = ip_pmf,
    h = forecast_horizon
  ),
  adapt_delta = 0.95,
  max_treedepth = 12,
  init = \() list(init_R = 1, rw_sd = 0.01) 
)

Finally, we extract the forecast samples:

pipeline_forecasts <- pipeline_forecast_fit |>
  gather_draws(forecast[day], ndraws = 100) |>
  ungroup() |>
  mutate(
    actual_day = day + max(nowcast_estimates$day),
    approach = "Pipeline"
  )

head(pipeline_forecasts)

# A tibble: 6 × 8
    day .chain .iteration .draw .variable .value actual_day approach
  <int>  <int>      <int> <int> <chr>      <dbl>      <int> <chr>   
1     1      2        358   858 forecast      38         62 Pipeline
2     1      2        188   688 forecast      35         62 Pipeline
3     1      3        394  1394 forecast      40         62 Pipeline
4     1      4        278  1778 forecast      41         62 Pipeline
5     1      1        393   393 forecast      38         62 Pipeline
6     1      2        443   943 forecast      58         62 Pipeline

We can now visualise the pipeline forecast results:

# Plot pipeline forecast from cutoff onwards
ggplot() +
  # Final observed data (truth) for evaluation period
  geom_point(data = complete_at_horizon |> 
               filter(day >= cutoff, day <= cutoff + forecast_horizon), 
            aes(x = day, y = complete_onsets), 
            color = "black", size = 1) +
  # Pipeline forecast ribbons from cutoff
  geom_line(data = pipeline_forecasts |>
              filter(actual_day >= cutoff, actual_day <= cutoff + forecast_horizon),
            aes(x = actual_day, y = .value, group = .draw),
            color = "blue", alpha = 0.1) +
  # Mark cutoff date
  geom_vline(xintercept = cutoff, 
             linetype = "dashed", color = "blue", linewidth = 1) +
  scale_y_log10() +
  xlim(cutoff, cutoff + forecast_horizon) +
  labs(
    x = "Day",
    y = "Onsets",
    title = "Pipeline approach: Forecasting from point nowcast",
    subtitle = "Blue line: cutoff (forecast start)"
  ) +
  theme_minimal()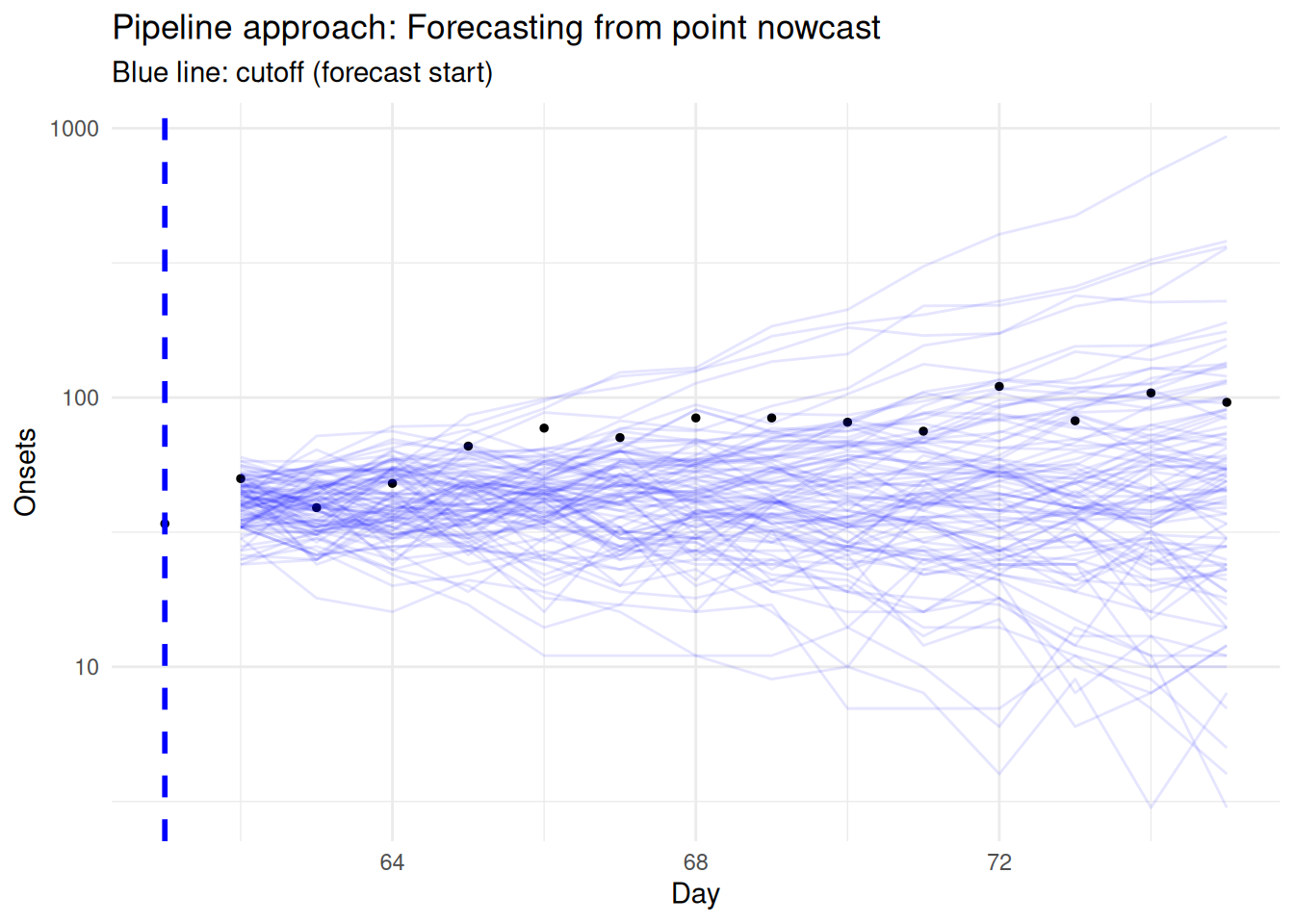

Take 5 minutes

Compare this pipeline approach to the complete data approach:

What additional information does it use?
What are the limitations of using point estimates from the nowcast?
How does this approach differ from the complete data approach?
How might model mismatch between the geometric and renewal models affect results?

Solution

What additional information does it use?

This approach uses all available data, including the recent truncated observations that were ignored in the complete data approach.

What are the limitations of using point estimates from the nowcast?

It doesn’t include the uncertainty from the nowcast, leading to overconfident predictions.
Point estimates ignore the full posterior distribution from the nowcasting step.

How does this approach differ from the complete data approach?

It has lower variance than the complete data approach due to using more information.
It appears slightly more biased towards under-predicting than the complete data approach.

How might model mismatch between the geometric and renewal models affect results?

The geometric random walk and renewal equation represent different generative processes (Lison et al. 2024), which can lead to inconsistencies as we saw in the joint nowcasting session.
This mismatch can create systematic biases and unrealistic uncertainty quantification.

Approach 3: Pipeline approach (with uncertainty)

This approach would sample from the nowcast posterior and then forecast from multiple trajectories. We describe the approach but don’t implement it as it’s computationally expensive.

The approach works as follows:

Sample multiple nowcast realisations: Instead of using point estimates from the geometric nowcast, we would sample 100+ different nowcast trajectories from the posterior distribution.
Forecast from each trajectory: For each of the 100+ nowcast samples, we would combine it with the older “complete” data and fit the renewal forecasting model separately.
Combine forecast distributions: We would then combine all the resulting forecast distributions to get final predictions that include some uncertainty from the nowcasting step.

Take 3 minutes

Consider this approach compared to Approaches 1 and 2:

What advantage does it have over the simple pipeline approach?
Why is it computationally expensive compared to a joint model?
What problem does it still have regarding model consistency?

Solution

Advantage: Unlike Approach 2, it propagates some uncertainty from the nowcast into the forecast, giving more realistic prediction intervals
Computational cost: Requires fitting the renewal model many times (once per nowcast sample), making it slow compared to a single joint model fit
Model mismatch remains: Still uses different generative processes (geometric for nowcast, renewal for forecast), creating inconsistencies (Lison et al. 2024)

Approach 4: Joint approach

This approach extends the joint nowcasting model to include forecasting, using a renewal process as the generative process throughout.

We start by loading the joint model:

joint_model <- nfidd_cmdstan_model("joint-nowcast-with-r")
joint_model

 1: functions {
 2:   #include "functions/geometric_random_walk.stan"
 3:   #include "functions/renewal.stan"
 4:   #include "functions/convolve_with_delay.stan"
 5:   #include "functions/observe_onsets_with_delay.stan"
 6:   #include "functions/combine_obs_with_predicted_obs_rng.stan"
 7: }
 8: 
 9: data {
10:   int n;                // number of days
11:   int m;                // number of reports
12:   array[n] int p;       // number of observations per day
13:   array[m] int obs;     // observed symptom onsets
14:   int d;                // number of reporting delays
15:   int gen_time_max;     // maximum generation time
16:   array[gen_time_max] real gen_time_pmf;  // pmf of generation time distribution
17:   int<lower = 1> ip_max; // max incubation period
18:   array[ip_max + 1] real ip_pmf;
19:   int h;                // number of days to forecast
20: }
21: 
22: transformed data{
23:   array[n] int P = to_int(cumulative_sum(p));
24:   array[n] int D = to_int(cumulative_sum(rep_array(d, n)));
25: }
26: 
27: parameters {
28:   real<lower = 0> init_I;         // initial number of infected
29:   real<lower = 0> init_R;         // initial reproduction number
30:   array[n-1] real rw_noise;       // random walk noise
31:   real<lower = 0> rw_sd; // random walk standard deviation
32:   simplex[d] reporting_delay; // reporting delay distribution
33: }
34: 
35: transformed parameters {
36:   array[n] real R = geometric_random_walk(init_R, rw_noise, rw_sd);
37:   array[n] real infections = renewal(init_I, R, gen_time_pmf);
38:   array[n] real onsets = convolve_with_delay(infections, ip_pmf);
39:   array[m] real onsets_by_report = observe_onsets_with_delay(onsets, reporting_delay, P, p);
40: }
41: 
42: model {
43:   // Prior
44:   init_I ~ lognormal(0, 1);
45:   init_R ~ normal(1, 0.5) T[0, ];
46:   rw_noise ~ std_normal();
47:   rw_sd ~ normal(0, 0.05) T[0,];
48:   reporting_delay ~ dirichlet(rep_vector(1, d));
49:   // Likelihood
50:   obs ~ poisson(onsets_by_report);
51: }
52: 
53: generated quantities {
54:   array[d*n] real complete_onsets_by_report = observe_onsets_with_delay(onsets, reporting_delay, D, rep_array(d, n));
55:   array[n] int nowcast = combine_obs_with_predicted_obs_rng(obs, complete_onsets_by_report, P, p, d, D);
56: 
57:   // Forecast the underlying onsets
58:   array[h] real forecast;
59:   if (h > 0) {
60:     array[h + n - 1] real f_rw_noise;
61:     for (i in 1:n-1) {
62:       f_rw_noise[i] = rw_noise[i];
63:     }
64:     for (i in n:(h + n - 1)) {
65:       f_rw_noise[i] = normal_rng(0, 1);
66:     }
67:     array[h + n] real f_R = geometric_random_walk(init_R, f_rw_noise, rw_sd);
68:     array[h + n] real f_infections = renewal(init_I, f_R, gen_time_pmf);
69:     array[h + n] real f_onsets = convolve_with_delay(f_infections, ip_pmf);
70:     for (i in 1:h) {
71:       forecast[i] = poisson_rng(f_onsets[n + i]);
72:     }
73:   }
74: }
75:

Take 3 minutes

What parts of the joint model allow for forecasting?

Solution

The joint model includes a generated quantities block that generates forecasts for future days using the same renewal process as for the observed data.
The parameter h specifies the number of days to forecast beyond the observed data.
In the generated quantities block, the model simulates future random walk noise, extends the \(R_t\) trajectory, and generates future infections and onsets.
Forecasts are then drawn from the predictive distribution for each future day, ensuring that both nowcasting and forecasting are handled within a single, consistent generative framework.
This is exactly the same as for the renewal_model as we are only forecasting the final number of onsets and not simulating the reporting process.

Now we fit the joint model with forecasting parameters:

joint_forecast_fit <- nfidd_sample(
  joint_model,
  data = list(
    n = length(unique(filtered_reporting_triangle$day)),
    m = nrow(filtered_reporting_triangle),
    p = filtered_reporting_triangle |>
     group_by(day) |>
     filter(d == max(d)) |>
     mutate(d = d + 1) |>
     pull(d),
    obs = filtered_reporting_triangle$reported_onsets,
    d = 16,
    gen_time_max = length(gen_time_pmf),
    gen_time_pmf = gen_time_pmf,
    ip_max = length(ip_pmf) - 1,
    ip_pmf = ip_pmf,
    h = forecast_horizon
  ),
  adapt_delta = 0.99,
  max_treedepth = 12,
  init = \() list(init_R = 1, rw_sd = 0.01) 
)

We extract the joint results for forecasting:

joint_forecasts <- joint_forecast_fit |>
  gather_draws(forecast[day], ndraws = 100) |>
  ungroup() |>
  mutate(
    actual_day = day + max(filtered_reporting_triangle$day),
    approach = "Joint"
  )

tail(joint_forecasts)

# A tibble: 6 × 8
    day .chain .iteration .draw .variable .value actual_day approach
  <int>  <int>      <int> <int> <chr>      <dbl>      <dbl> <chr>   
1    14      2        173   673 forecast     226         75 Joint   
2    14      3        300  1300 forecast     273         75 Joint   
3    14      4        154  1654 forecast     802         75 Joint   
4    14      3         70  1070 forecast     153         75 Joint   
5    14      2        192   692 forecast     283         75 Joint   
6    14      3        410  1410 forecast      94         75 Joint

Finally, let’s visualise the joint nowcast results:

# Plot joint forecast from cutoff onwards
forecast_start_day <- cutoff
forecast_end_day <- cutoff + forecast_horizon

ggplot() +
  # Final observed data (truth) for evaluation period
  geom_point(data = complete_at_horizon |> 
               filter(day >= forecast_start_day, day <= forecast_end_day), 
            aes(x = day, y = complete_onsets), 
            color = "black", size = 1) +
  # Joint model forecast ribbons from cutoff
  geom_line(data = joint_forecasts |>
              filter(actual_day >= forecast_start_day, actual_day <= forecast_end_day),
            aes(x = actual_day, y = .value, group = .draw),
            color = "purple", alpha = 0.1) +
  # Mark cutoff date
  geom_vline(xintercept = cutoff, 
             linetype = "dashed", color = "blue", linewidth = 1) +
  scale_y_log10() +
  xlim(forecast_start_day, forecast_end_day) +
  labs(
    x = "Day",
    y = "Onsets",
    title = "Joint approach: Forecasting from joint nowcast and forecast",
    subtitle = "Blue line: cutoff (forecast start)"
  ) +
  theme_minimal()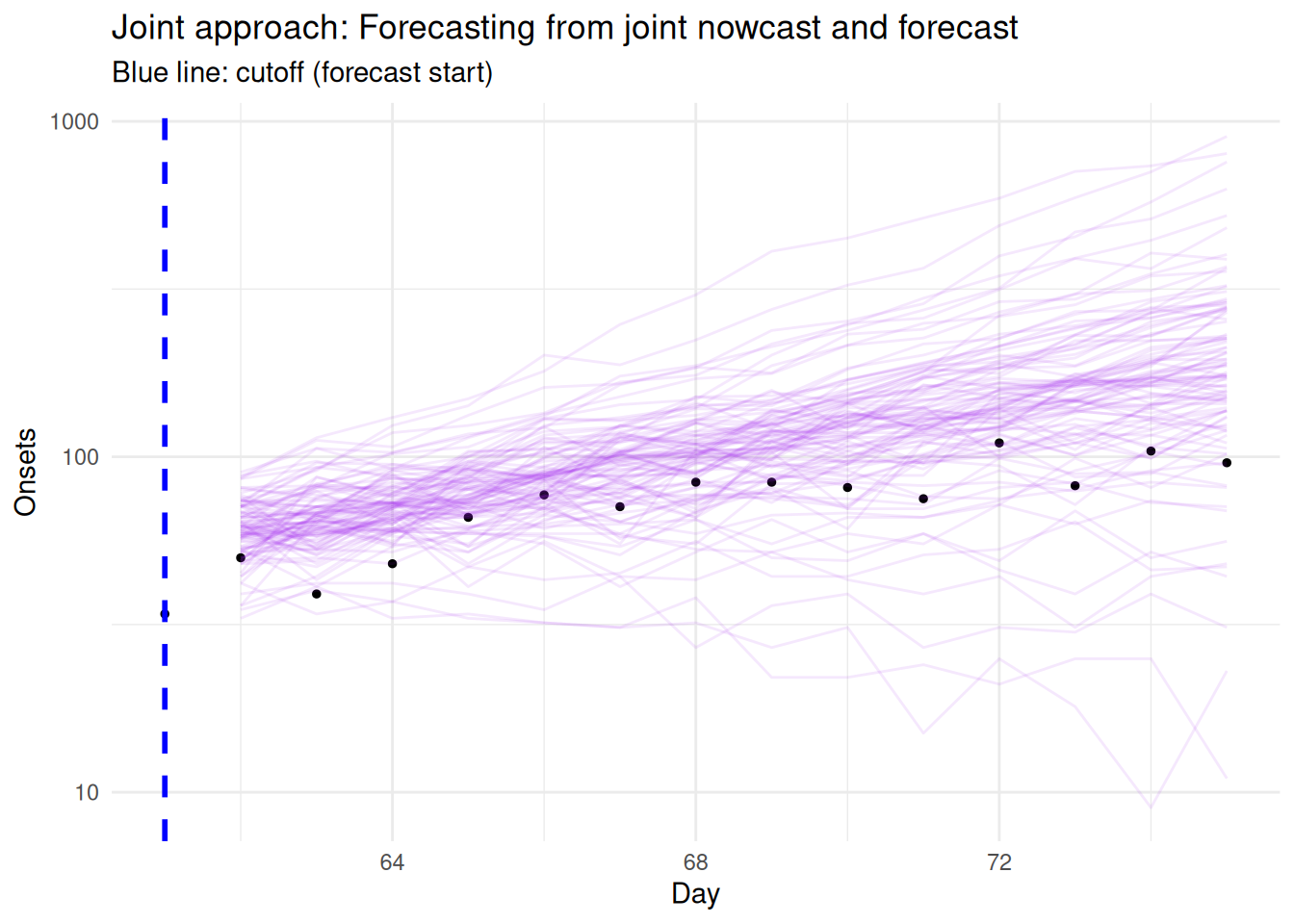

Take 5 minutes

What are the advantages of the joint model approach?

How does it address the model mismatch problem?
What uncertainties does it properly account for?
Why might it perform better than the pipeline and complete data approaches?
Why might it perform worse than the complete data approach?

Solution

How does it address the model mismatch problem?
The joint model uses a single consistent generative process, such as the renewal equation, for both nowcasting and forecasting.
This avoids the mismatch that can occur when different models are used for each task, for example, using a geometric random walk for forecasting and a renewal process for nowcasting.
By using the same model structure throughout, the joint approach ensures that assumptions about transmission and reporting are aligned across all time points.
What uncertainties does it properly account for?
The joint model propagates all relevant sources of uncertainty, including those from reporting delays, nowcast estimates, and the evolution of \(R_t\).
It also accounts for the correlation between uncertainty in the nowcast and the forecast, which can be important for accurate prediction intervals.
This means that the uncertainty in the most recent data, which is incomplete, is properly reflected in the forecast.
Why might it perform better than the pipeline and complete data approaches?
The joint model can perform better because it uses all available data, including the most recent but incomplete reports, and models the process that generates both the observed and unobserved data.
This allows it to make use of information that the pipeline approach, which separates nowcasting and forecasting, might miss.
By jointly modelling the entire process, it can provide more coherent and potentially more accurate forecasts, especially when the reporting process is well understood.
Why might it perform worse than the complete data approach?
In some situations, the complete data approach, which waits for older data to become nearly complete before forecasting, might perform better.
This can happen if the most recent data are highly incomplete or unrepresentative, for example, due to sudden changes in reporting or the epidemic process.
In such cases, older data may provide a more stable basis for forecasting, even though it is less timely.
It may also underperform if the generative process is not consistent with the data we have. For example, if the growth rate of older data happens to be more consistent with the future growth rate of the epidemic, then the complete data approach will perform better. These issues indicate that the underlying generative process or forecast model could be improved to better capture changes in the epidemic or reporting dynamics.

Evaluation and comparison

We’ll evaluate all four approaches against what will finally be reported (our complete_at_horizon dataset) using proper scoring rules.

Prepare evaluation data

# Create evaluation dataset - what we're forecasting against
evaluation_data <- complete_at_horizon |>
  filter(day > cutoff, day <= cutoff + forecast_horizon) |>
  mutate(
    forecast_horizon = day - cutoff,
    observed = complete_onsets
  ) |>
  select(day, forecast_horizon, observed)

head(evaluation_data)

# A tibble: 6 × 3
    day forecast_horizon observed
  <dbl>            <dbl>    <int>
1    62                1       50
2    63                2       39
3    64                3       48
4    65                4       66
5    66                5       77
6    67                6       71

Visualise all the forecasts together

As in all other sessions, we first visualise the forecasts together.

forecast_results <- bind_rows(
  complete_data_forecasts |>
    filter(actual_day > cutoff),
  pipeline_forecasts,
  joint_forecasts
)

forecast_results |>
  ggplot(aes(x = actual_day, y = .value, group = .draw, color = approach)) +
  geom_line(alpha = 0.1) +
  geom_point(data = evaluation_data, aes(x = day, y = observed, group = NULL, color = NULL), color = "black", size = 1) +
  scale_y_log10() +
  labs(x = "Day", y = "Onsets", title = "All forecast approaches") +
  theme_minimal() +
  guides(color = guide_legend(
    title = "Approach", override.aes = list(alpha = 1, linewidth = 1))
  ) +
  theme(legend.position = "bottom") +
  facet_wrap(vars(approach), ncol = 1)

Warning in scale_y_log10(): log-10 transformation introduced infinite values.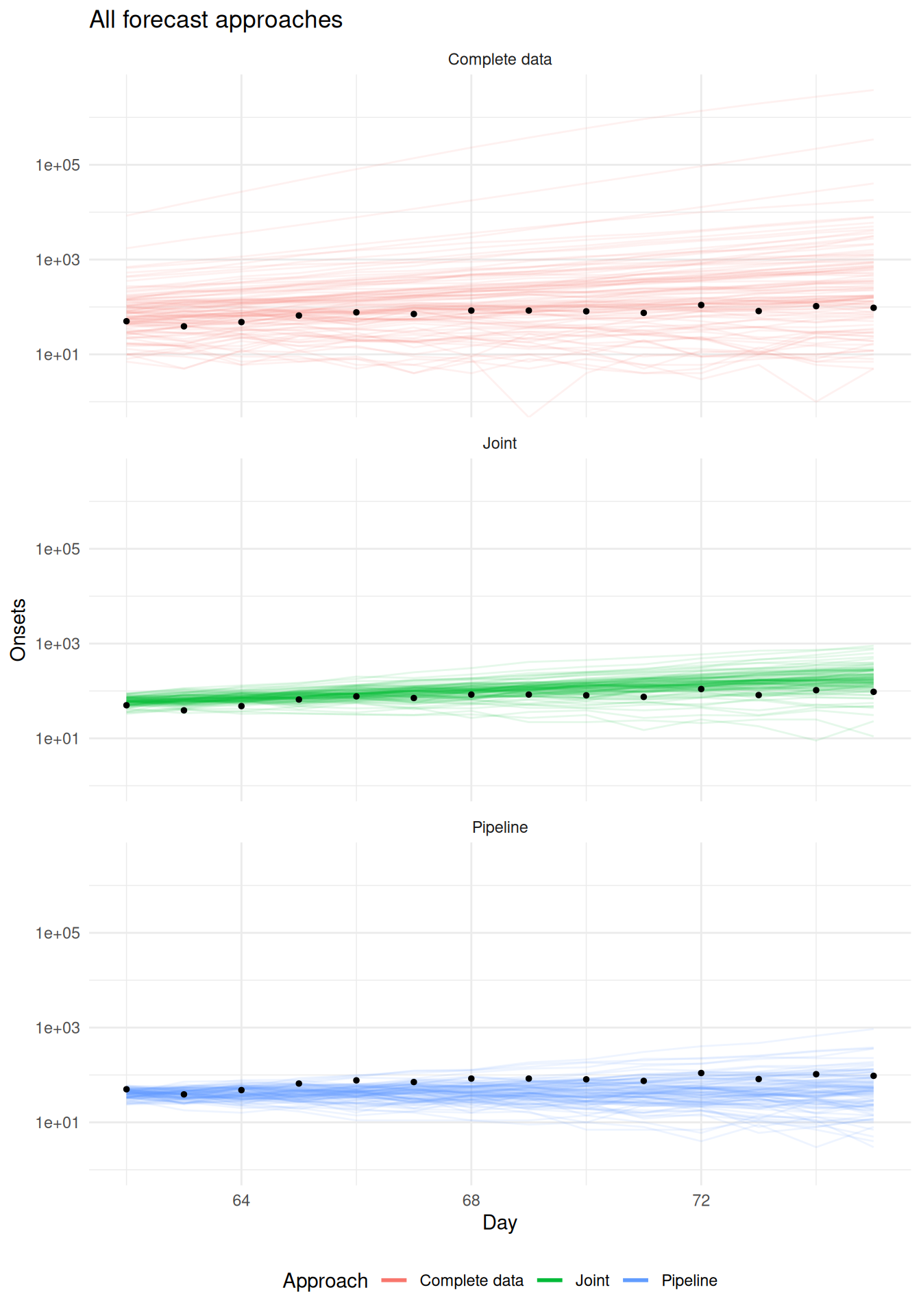

Quantitative evaluation using scoringutils

Using scoringutils, We first create a forecast sample object

sc_forecasts <- forecast_results |>
    left_join(evaluation_data, by = c("actual_day" = "day")) |>
    group_by(approach, actual_day) |>
    mutate(
      .draw = row_number()
    ) |>
    as_forecast_sample(
      forecast_unit = c("approach", "actual_day"),
      observed = "observed",
      predicted = ".value",
      sample_id = ".draw"
    )
sc_forecasts

Forecast type: sample

Forecast unit:

approach and actual_day


      sample_id predicted observed      approach actual_day
          <int>     <num>    <int>        <char>      <num>
   1:         1        83       50 Complete data         62
   2:         2       145       50 Complete data         62
   3:         3       108       50 Complete data         62
   4:         4        31       50 Complete data         62
   5:         5       150       50 Complete data         62
  ---                                                      
4196:        96       273       96         Joint         75
4197:        97       802       96         Joint         75
4198:        98       153       96         Joint         75
4199:        99       283       96         Joint         75
4200:       100        94       96         Joint         75

and then calculate the scores:

scores <- sc_forecasts |>
  score()

head(scores)

        approach actual_day  bias      dss    crps overprediction
          <char>      <num> <num>    <num>   <num>          <num>
1: Complete data         62  0.25 13.53014 20.4381           1.78
2: Complete data         63  0.49 14.69952 30.4814           7.50
3: Complete data         64  0.40 15.81995 34.4264           6.48
4: Complete data         65  0.28 16.93241 38.0538           2.36
5: Complete data         66  0.12 18.00671 47.8366           0.36
6: Complete data         67  0.33 19.06576 66.0303           6.40
   underprediction dispersion log_score      mad ae_median    se_mean
             <num>      <num>     <num>    <num>     <num>      <num>
1:               0    18.6581  4.983849  55.5975      15.0   23565.32
2:               0    22.9814  5.110518  64.4931      29.0   66594.96
3:               0    27.9464  5.188909  71.9061      27.5  158913.85
4:               0    35.6938  5.315048  83.0256      17.0  395238.54
5:               0    47.4766  5.524244  94.1451      10.0 1024224.96
6:               0    59.6303  5.665452 114.1602      37.0 2764006.00

Overall performance table

We summarise the performance across all forecast horizons:

# Create summary table showing overall performance
overall_performance <- scores |>
  summarise_scores(by = "approach") |>
  arrange(crps)

knitr::kable(overall_performance, 
             caption = "Overall forecast performance by approach",
             digits = 3)

Overall forecast performance by approach
approach	bias	dss	crps	overprediction	underprediction	dispersion	log_score	mad	ae_median	se_mean
Pipeline	-0.671	7.814	21.318	0.003	16.054	5.260	5.299	20.333	33.643	8.005450e+02
Joint	0.654	8.372	23.215	14.151	0.000	9.064	4.972	36.641	34.893	3.014737e+03
Complete data	0.325	20.203	193.802	6.913	0.000	186.889	5.898	137.564	39.536	2.580990e+08

Performance by forecast horizon

We examine how performance varies with forecast horizon:

# Calculate performance by horizon
horizon_performance <- scores |>
  summarise_scores(by = c("approach", "actual_day"))

# Plot showing how performance varies by forecast horizon
ggplot(horizon_performance) +
  aes(x = actual_day, y = crps, color = approach) +
  geom_line(linewidth = 1) +
  geom_point(size = 1) +
  scale_y_log10() +
  labs(
    x = "Forecast horizon (days)",
    y = "CRPS (lower is better)",
    title = "Forecast performance by horizon",
    color = "Approach"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")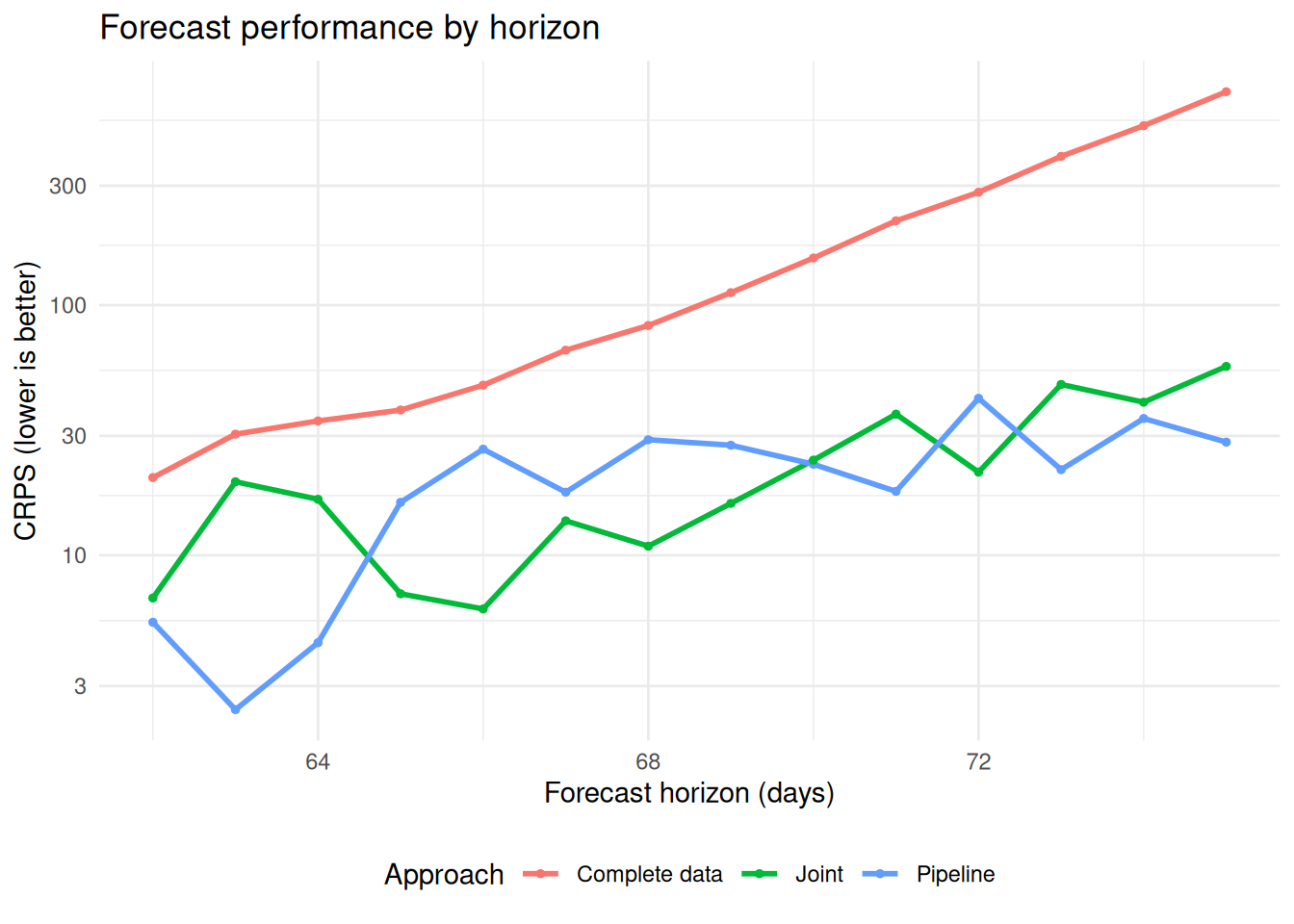

Take 5 minutes

Compare the four approaches across the evaluation metrics

Solution

Note these results are stochastic. Why is this?

From this evaluation, we can see:

Complete data approach: Performs much worse overall. Performance degrades rapidly with longer forecast horizons.
Joint approach: Has comparable performance to the pipeline approach with some overprediction bias and higher dispersion, indicating greater uncertainty.
Pipeline approach: Has some systematic underprediction bias, performs best at early and late forecast horizons, and performs worse at medium forecast horizons

To really understand the performance difference we would need to evaluate across multiple forecast dates.

Going further

Challenge

Try implementing the pipeline approach with uncertainty propagation by sampling multiple nowcast trajectories and fitting the renewal model to each. How does this compare computationally and in terms of forecast accuracy to the other approaches?
Experiment with different forecast horizons (7 days, 21 days, 28 days). How does the relative performance of each approach change with longer forecast horizons?
Compare the approaches when there are changes in transmission (e.g., at different cut off dates) near the forecast date. Which methods are more robust to such changes?

Methods in practice

Several packages implement these concepts:

EpiNow2: Pipeline nowcasting and forecasting
epinowcast: Joint nowcasting and forecasting in an efficient framework

Research has demonstrated that joint modelling of data sources provides significant advantages over combining estimates from separate models (Lison et al. 2024) when evaluating multiple nowcast dates. In practice, implementations often include hierarchical models for multiple locations, time-varying delays, and ensemble approaches for robustness.

Wrap up

Review what you’ve learned in this session with the learning objectives
Share your questions and thoughts

References

Lison, Adrian, Sam Abbott, Jana Huisman, and Tanja Stadler. 2024. “Generative Bayesian Modeling to Nowcast the Effective Reproduction Number from Line List Data with Missing Symptom Onset Dates.” PLOS Computational Biology 20 (4): e1012021. https://doi.org/10.1371/journal.pcbi.1012021.