library("nfidd")
library("dplyr")
library("tidyr")
library("ggplot2")
library("tidybayes")
library("scoringutils")Forecasting models
Introduction
We can classify models along a spectrum by how much they include an understanding of underlying processes, or mechanisms; or whether they emphasise drawing from the data using a statistical approach. In this session, we’ll start with the renewal model that we’ve been using and explore adding both more mechanistic structure and then more statistical structure to the model. We’ll again evaluate these models to see what effect these different approaches might have.
Slides
Objectives
The aim of this session is to introduce some common forecasting models and to evaluate them.
Caution
None of the models introduced in this section are designed for real-world outbreak use!
Setup
Source file
The source file of this session is located at sessions/forecasting-models.qmd.
Libraries used
In this session we will use the nfidd package to load a data set of infection times and access stan models and helper functions, the dplyr and tidyr packages for data wrangling, ggplot2 library for plotting, the tidybayes package for extracting results of the inference and the scoringutils package for evaluating forecasts.
Tip
The best way to interact with the material is via the Visual Editor of RStudio.
Initialisation
We set a random seed for reproducibility. Setting this ensures that you should get exactly the same results on your computer as we do. We also set an option that makes cmdstanr show line numbers when printing model code. This is not strictly necessary but will help us talk about the models.
set.seed(123)
options(cmdstanr_print_line_numbers = TRUE)What did we learn about the random walk model from the forecasting concepts session?
- It was unbiased when the reproduction number was approximately constant but when the reproduction number was reducing due to susceptible depletion, the random walk model overestimated the number of cases systematically.
- It did relatively well at short-term forecasting indicating that it was capturing some of the underlying dynamics of the data generating process.
What did a geometric random walk model look like again?
R <- geometric_random_walk(init = 1, noise = rnorm(100), std = 0.1)
data <- tibble(t = seq_along(R), R = exp(R))
ggplot(data, aes(x = t, y = R)) +
geom_line() +
labs(title = "Simulated data from a random walk model",
x = "Time",
y = "R")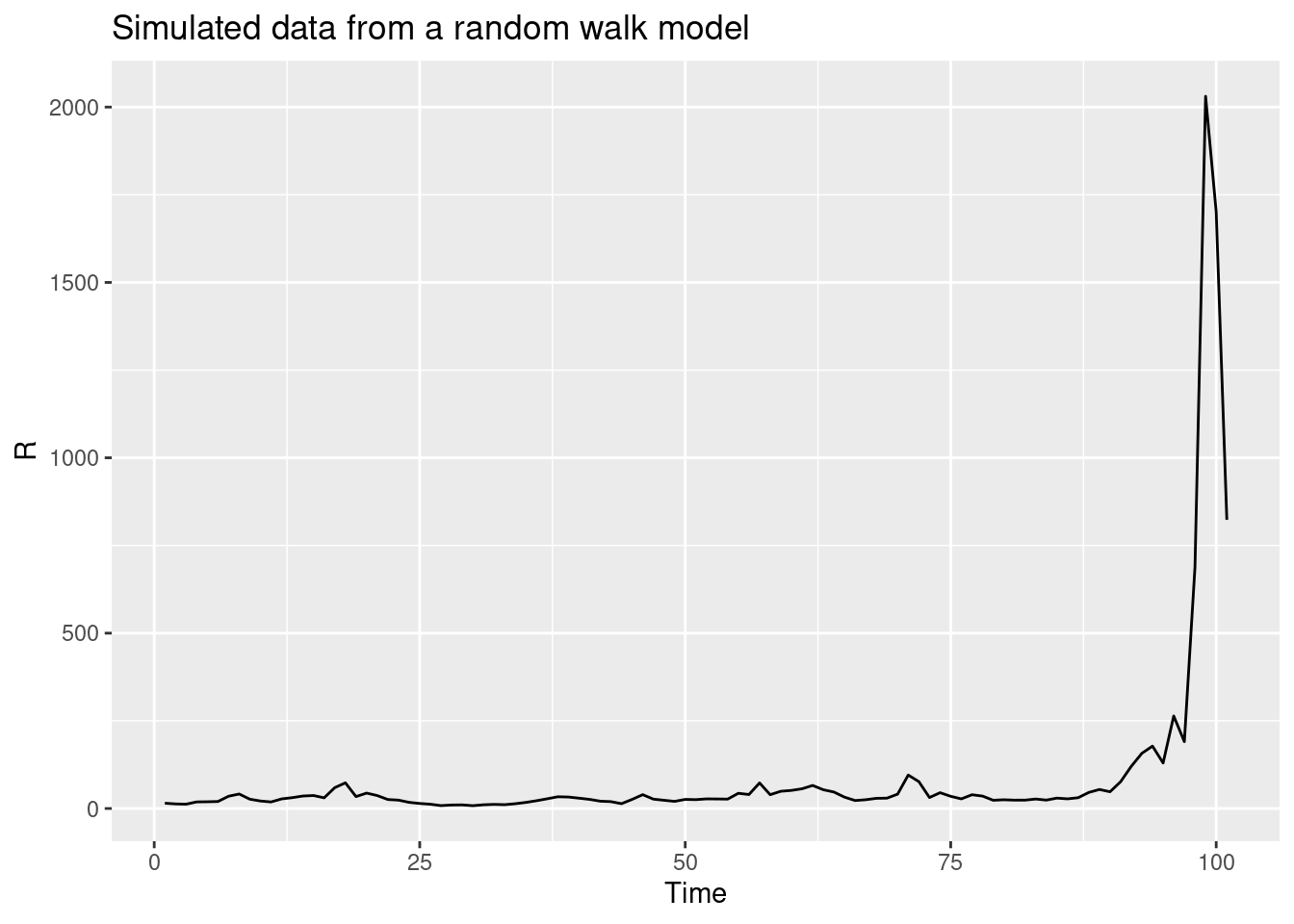
Forecasting models as a spectrum
A large part of this course has been about showing the importance of understanding and modelling the underlying mechanisms of the data generating process. However, in many forecasting scenarios, we may not have a good understanding of the underlying mechanisms, or the data may be too noisy to make accurate predictions. The worst case is that we have mistaken beliefs about the underlying mechanisms and use these to make predictions which are systematically wrong and misleading. In these cases, forecasters often use statistical models to make predictions which have little or no mechanistic basis. In our work, we have found that a combination of mechanistic and statistical models can be very powerful but that identifying the best model for a given forecasting task can be challenging.
Adding more mechanistic structure to the renewal model
One way to potentially improve the renewal model is to add more mechanistic structure. In the forecasting concepts session, we saw that the renewal model was making unbiased forecasts when the reproduction number was constant but that it overestimated the number of cases when the reproduction number was reducing due to susceptible depletion.
Warning
This is slightly cheating as we know the future of this outbreak and so can make a model to match. This is easy to do and important to watch for if wanting to make generalisable methods.
This suggests that we should add a term to the renewal model which captures the depletion of susceptibles. One way to do this is to add a term which is proportional to the number of susceptibles in the population. This is the idea behind the SIR model which is a simple compartmental model of infectious disease transmission. If we assume that susceptible depletion is the only mechanism which is causing the reproduction number to change, we can write the reproduction model as:
\[ R_t = \frac{S_{t-1}}{N} R_0 \]
Note
This approximates susceptible depletion as a linear function of the number of susceptibles in the population. This is a simplification but it is a good starting point.
What behaviour would we expect from this model?
n <- 100
N <- 1000
R0 <- 1.5
S <- rep(NA, n)
S[1] <- N
Rt <- rep(NA, n) ## reproduction number
Rt[1] <- R0
I <- rep(NA, n)
I[1] <- 1
for (i in 2:n) {
Rt[i] <- (S[i-1]) / N * R0
I[i] <- I[i-1] * Rt[i]
S[i] <- S[i-1] - I[i]
}
data <- tibble(t = 1:n, Rt = Rt)
ggplot(data, aes(x = t, y = Rt)) +
geom_line() +
labs(title = "Simulated data from an SIR model",
x = "Time",
y = "Rt")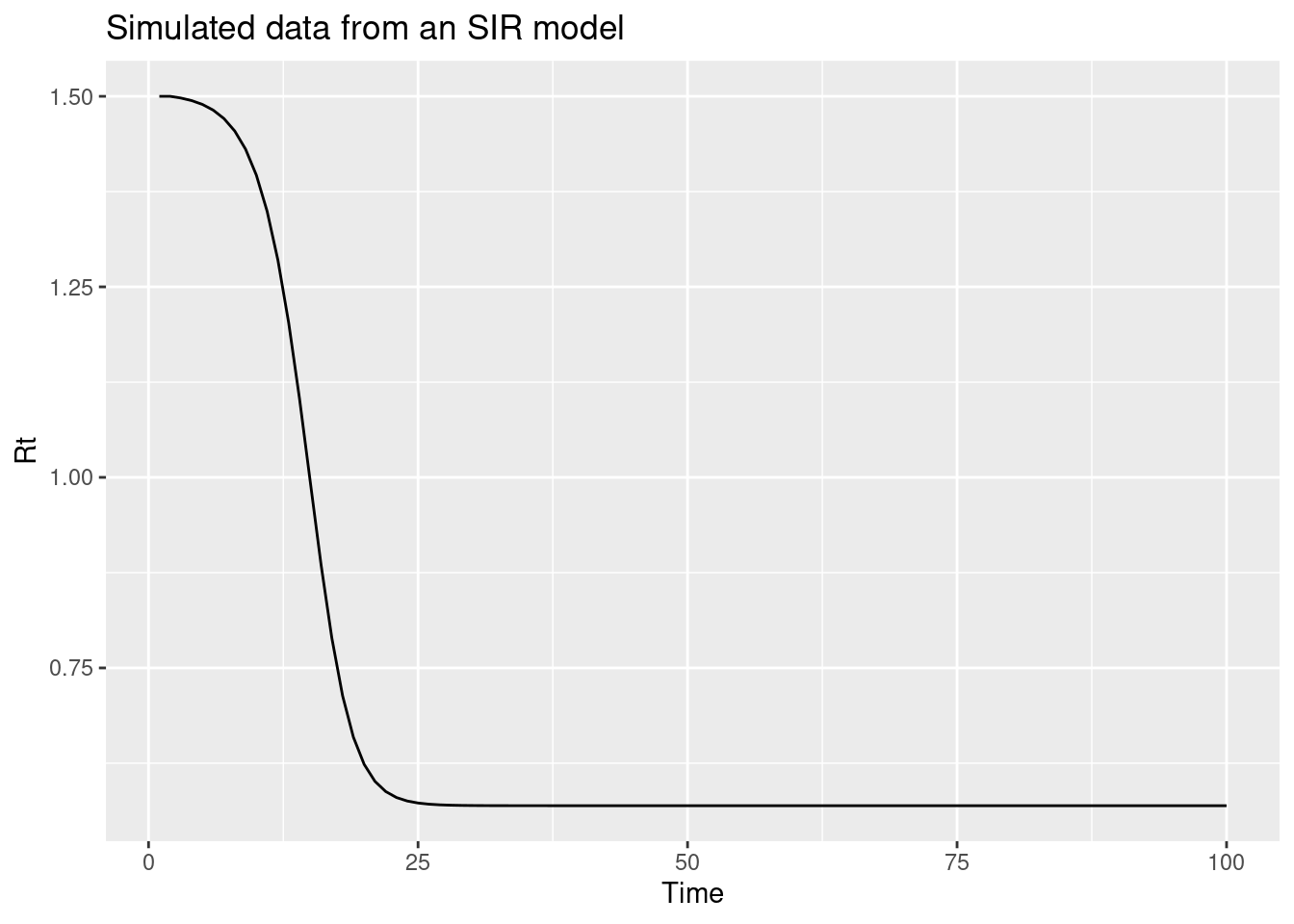
The key assumptions we are making here are:
- The population is constant and we roughly know the size of the population.
- The reproduction number only changes due to susceptible depletion
- The number of new cases at each time is proportional to the number of susceptibles in the population.
We’ve coded this up as a stan model in stan/mechanistic-r.stan. See stan/functions/pop_bounded_renewal.stan for the function which calculates the reproduction number. Let’s load the model:
mech_mod <- nfidd_cmdstan_model("mechanistic-r")
mech_mod 1: functions {
2: #include "functions/convolve_with_delay.stan"
3: #include "functions/pop_bounded_renewal.stan"
4: }
5:
6: data {
7: int n; // number of days
8: int I0; // number initially infected
9: array[n] int obs; // observed symptom onsets
10: int gen_time_max; // maximum generation time
11: array[gen_time_max] real gen_time_pmf; // pmf of generation time distribution
12: int<lower = 1> ip_max; // max incubation period
13: array[ip_max + 1] real ip_pmf;
14: int h; // number of days to forecast
15: array[2] real N_prior; // prior for total population
16: }
17:
18: transformed data {
19: int m = n + h;
20: }
21:
22: parameters {
23: real<lower = 0> R; // initial reproduction number
24: real<lower = 0> N; // total population
25: }
26:
27: transformed parameters {
28: array[m] real infections = pop_bounded_renewal(I0, R, gen_time_pmf, N, m);
29: array[m] real onsets = convolve_with_delay(infections, ip_pmf);
30: }
31:
32: model {
33: // priors
34: R ~ normal(1, 0.5) T[0,];
35: N ~ normal(N_prior[1], N_prior[2]) T[0,];
36: obs ~ poisson(onsets[1:n]);
37: }
38:
39: generated quantities {
40: array[h] real forecast;
41: if (h > 0) {
42: for (i in 1:h) {
43: forecast[i] = poisson_rng(onsets[n + i]);
44: }
45: }
46: }Adding more statistical structure to the renewal model
Adding more mechanistic structure is not always possible and, if we don’t specify mechanisms correctly, might make forecasts worse. Rather than adding more mechanistic structure to the renewal model, we could add more statistical structure with the aim of improving performance. Before we do this, we need to think about what we want from a forecasting model. As we identified above, we want a model which is unbiased and which has good short-term forecasting properties. We know that we want it to be able to adapt to trends in the reproduction number and that we want it to be able to capture the noise in the data. A statistical term that can be used to describe a time series with a trend is saying that the time series is non-stationary. More specifically, a stationary time series is defined as one whose statistical properties, such as mean and variance, do not change over time. In infectious disease epidemiology, this would only be expected for endemic diseases without external seasonal influence.
The random walk model we used in the forecasting concept session is a special case of a more general class of models called autoregressive (AR) models. AR models are a class of models which predict the next value in a time series as a linear combination of the previous values in the time series. The random walk model is specifically a special case of an AR(1) model where the next value in the time series is predicted as the previous value, multiplied by a value between 1 and -1 , plus some noise. This becomes a random walk when the multipled value is 0.
For the log-transformed reproduction number (\(log(R_t)\)), the model is:
\[ log(R_t) = \phi log(R_{t-1}) + \epsilon_t \]
where \(\epsilon_t\) is a normally distributed error term with mean 0 and standard deviation \(\sigma\) and \(\phi\) is a parameter between -1 and 1. If we restrict \(\phi\) to be between 0 and 1, we get a model which is biased towards a reproduction number of 1 but which can still capture trends in the data that decay over time.
What behaviour would we expect from this model?
n <- 100
phi <- 0.4
sigma <- 0.1
log_R <- rep(NA, n)
log_R[1] <- rnorm(1, 0, sigma)
for (i in 2:n) {
log_R[i] <- phi * log_R[i-1] + rnorm(1, 0, sigma)
}
data <- tibble(t = 1:n, R = exp(log_R))
ggplot(data, aes(x = t, y = R)) +
geom_line() +
labs(title = "Simulated data from an exponentiated AR(1) model",
x = "Time",
y = "R")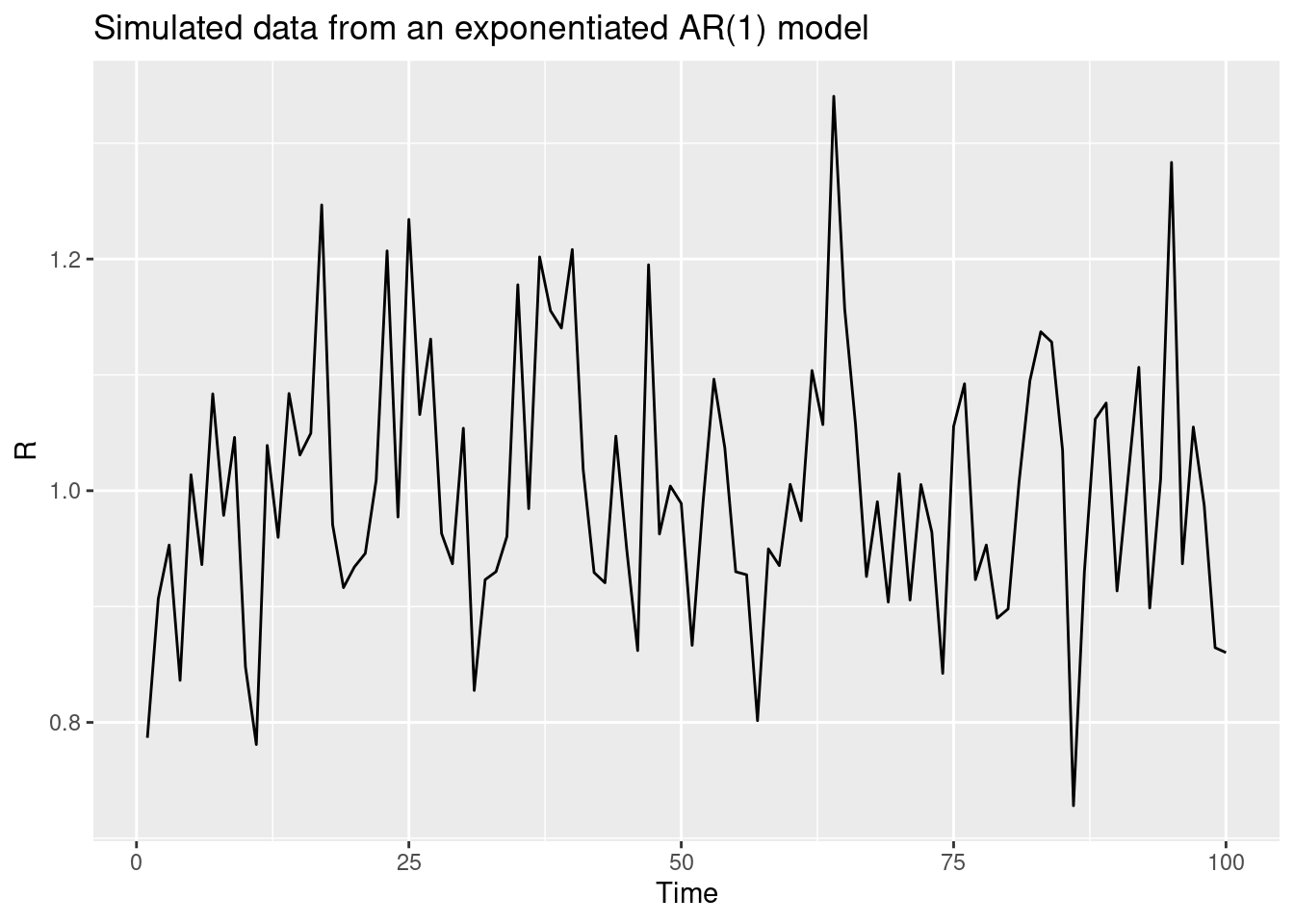
However, we probably don’t want a model which is biased towards a reproduction number of 1 (unless we have good reason to believe that is the expected behaviour). So what should we do?
Returning to the idea that the reproduction number is a non-stationary time series, as we expect to have a trend in the reproduction numbers we want to capture, we can use a method from the field of time series analysis called differencing to make the time series stationary. This involves taking the difference between consecutive values in the time series. For the log-transformed reproduction number, this would be:
\[ log(R_t) - log(R_{t-1}) = \phi (log(R_{t-1}) - log(R_{t-2})) + \epsilon_t \]
What behaviour would we expect from this model?
Again we look at an R function that implements this model:
geometric_diff_arfunction (init, noise, std, damp)
{
n <- length(noise) + 1
x <- numeric(n)
x[1] <- init
x[2] <- x[1] + noise[1] * std
for (i in 3:n) {
x[i] <- x[i - 1] + damp * (x[i - 1] - x[i - 2]) + noise[i -
1] * std
}
return(exp(x))
}
<bytecode: 0x560e18dbcc08>
<environment: namespace:nfidd>We can use this function to simulate a differenced AR process:
log_R <- geometric_diff_ar(init = 1, noise = rnorm(100), std = 0.1, damp = 0.1)
data <- tibble(t = seq_along(log_R), R = exp(log_R))
ggplot(data, aes(x = t, y = R)) +
geom_line() +
labs(title = "Simulated data from an exponentiated AR(1) model with differencing",
x = "Time",
y = "R")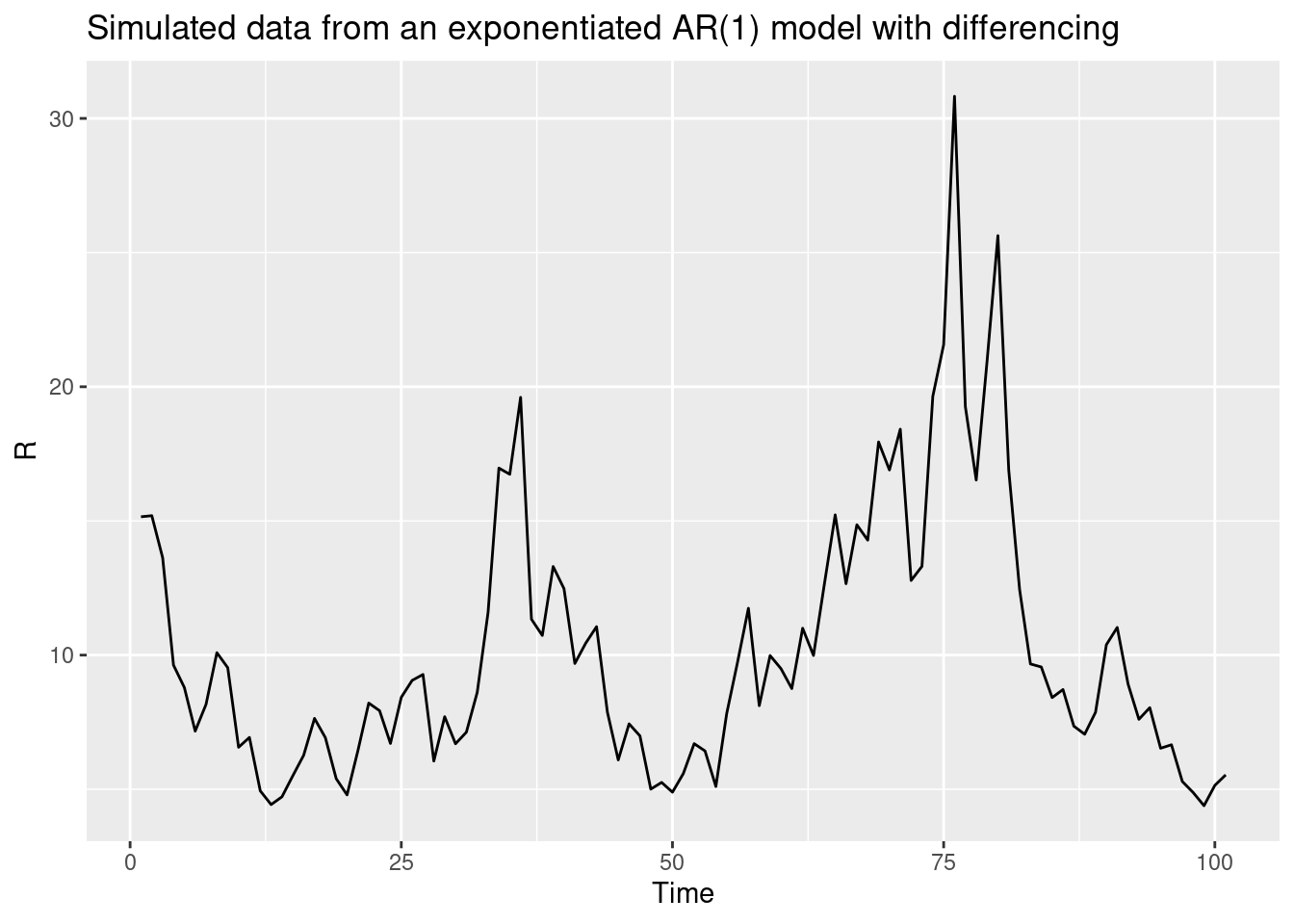
We’ve coded up a model that uses this differenced AR process as a stan model in stan/statistical-r.stan. See stan/functions/geometic_diff_ar.stan for the function which calculates the reproduction number. Lets load the model:
stat_mod <- nfidd_cmdstan_model("statistical-r")
stat_mod 1: functions {
2: #include "functions/convolve_with_delay.stan"
3: #include "functions/renewal.stan"
4: #include "functions/geometric_diff_ar.stan"
5: }
6:
7: data {
8: int n; // number of days
9: int I0; // number initially infected
10: array[n] int obs; // observed symptom onsets
11: int gen_time_max; // maximum generation time
12: array[gen_time_max] real gen_time_pmf; // pmf of generation time distribution
13: int<lower = 1> ip_max; // max incubation period
14: array[ip_max + 1] real ip_pmf;
15: int h; // number of days to forecast
16: }
17:
18: transformed data {
19: int m = n + h;
20: }
21:
22: parameters {
23: real init_R; // initial reproduction number
24: array[m-1] real rw_noise; // random walk noise
25: real<lower = 0> rw_sd; // random walk standard deviation
26: real<lower = 0, upper = 1> damp; // damping
27: }
28:
29: transformed parameters {
30: array[m] real R = geometric_diff_ar(init_R, rw_noise, rw_sd, damp);
31: array[m] real <upper = 1e5> infections = renewal(I0, R, gen_time_pmf);
32: array[m] real onsets = convolve_with_delay(infections, ip_pmf);
33: }
34:
35: model {
36: // priors
37: init_R ~ normal(-.1, 0.5); // Approximately Normal(1, 0.5)
38: rw_noise ~ std_normal();
39: rw_sd ~ normal(0, 0.01) T[0,];
40: damp ~ normal(1, 0.05) T[0, 1];
41: obs ~ poisson(onsets[1:n]);
42: }
43:
44: generated quantities {
45: array[h] real forecast;
46: if (h > 0) {
47: for (i in 1:h) {
48: forecast[i] = poisson_rng(onsets[n + i]);
49: }
50: }
51: }Forecasting with the mechanistic and statistical models
We will now use the mechanistic and statistical models to forecast the number of cases in the future using data simulated in the same way as we did in the forecasting concepts session. We will first load in the data and filter for a target forecast date.
gen_time_pmf <- make_gen_time_pmf()
ip_pmf <- make_ip_pmf()
onset_df <- simulate_onsets(
make_daily_infections(infection_times), gen_time_pmf, ip_pmf
)
onset_df# A tibble: 142 × 3
day onsets infections
<dbl> <int> <int>
1 1 0 0
2 2 0 1
3 3 0 0
4 4 0 2
5 5 0 1
6 6 0 1
7 7 0 1
8 8 0 3
9 9 0 0
10 10 3 0
# ℹ 132 more rows# we'll make a forecast on day non day 41, pretending we haven't seen the later
# data
cutoff <- 41
filtered_onset_df <- onset_df |>
filter(day <= cutoff)We will now fit the more mechanistic model to the data.
horizon <- 28
data <- list(
n = nrow(filtered_onset_df),
I0 = 1,
obs = filtered_onset_df$onsets,
gen_time_max = length(gen_time_pmf),
gen_time_pmf = gen_time_pmf,
ip_max = length(ip_pmf) - 1,
ip_pmf = ip_pmf,
h = horizon, # Here we set the number of days to forecast into the future
N_prior = c(10000, 2000) # the prior for the population size
)
mech_forecast_fit <- mech_mod$sample(
data = data, parallel_chains = 4
)mech_forecast_fit variable mean median sd mad q5 q95 rhat ess_bulk
lp__ 80.80 81.12 1.05 0.76 78.76 81.80 1.00 1624
R 1.49 1.49 0.02 0.02 1.46 1.52 1.00 3200
N 10019.91 10018.50 2030.55 1971.55 6644.10 13324.07 1.00 3293
infections[1] 0.10 0.10 0.00 0.00 0.10 0.10 1.00 3200
infections[2] 0.27 0.27 0.00 0.00 0.26 0.27 1.00 3200
infections[3] 0.38 0.38 0.00 0.00 0.37 0.39 1.00 3200
infections[4] 0.43 0.43 0.01 0.01 0.42 0.44 1.00 3200
infections[5] 0.47 0.47 0.01 0.01 0.45 0.48 1.00 3201
infections[6] 0.52 0.52 0.01 0.01 0.50 0.53 1.00 3200
infections[7] 0.57 0.57 0.01 0.01 0.55 0.60 1.00 3200
ess_tail
1919
2725
1980
2725
2725
2725
2725
2725
2725
2725
# showing 10 of 169 rows (change via 'max_rows' argument or 'cmdstanr_max_rows' option)We will now fit the more statistical model to the data.
data <- list(
n = nrow(filtered_onset_df),
I0 = 1,
obs = filtered_onset_df$onsets,
gen_time_max = length(gen_time_pmf),
gen_time_pmf = gen_time_pmf,
ip_max = length(ip_pmf) - 1,
ip_pmf = ip_pmf,
h = horizon # Here we set the number of days to forecast into the future
)
stat_forecast_fit <- stat_mod$sample(
data = data, parallel_chains = 4,
# again set the initial values to make fitting more numerically stable
init = \() list(init_R = 0, rw_sd = 0.01)
)Finally, we can extract the forecasts from the models and plot them.
mech_forecast <- mech_forecast_fit |>
gather_draws(forecast[day]) |>
ungroup() |>
mutate(day = day + cutoff)
stat_forecast <- stat_forecast_fit |>
gather_draws(forecast[day]) |>
ungroup() |>
mutate(day = day + cutoff)
forecast <- bind_rows(
mutate(mech_forecast, model = "more mechanistic"),
mutate(stat_forecast, model = "more statistical")
) |>
ungroup()
target_onsets <- onset_df |>
filter(day > cutoff) |>
filter(day <= cutoff + horizon)forecast |>
filter(.draw %in% sample(.draw, 100)) |>
ggplot(aes(x = day)) +
geom_line(
alpha = 0.1,
aes(y = .value, group = interaction(.draw, model), colour = model)
) +
geom_point(data = target_onsets, aes(x = day, y = onsets), color = "black") +
guides(colour = guide_legend(override.aes = list(alpha = 1))) +
lims(y = c(0, 500))Warning: Removed 74 rows containing missing values or values outside the scale range
(`geom_line()`).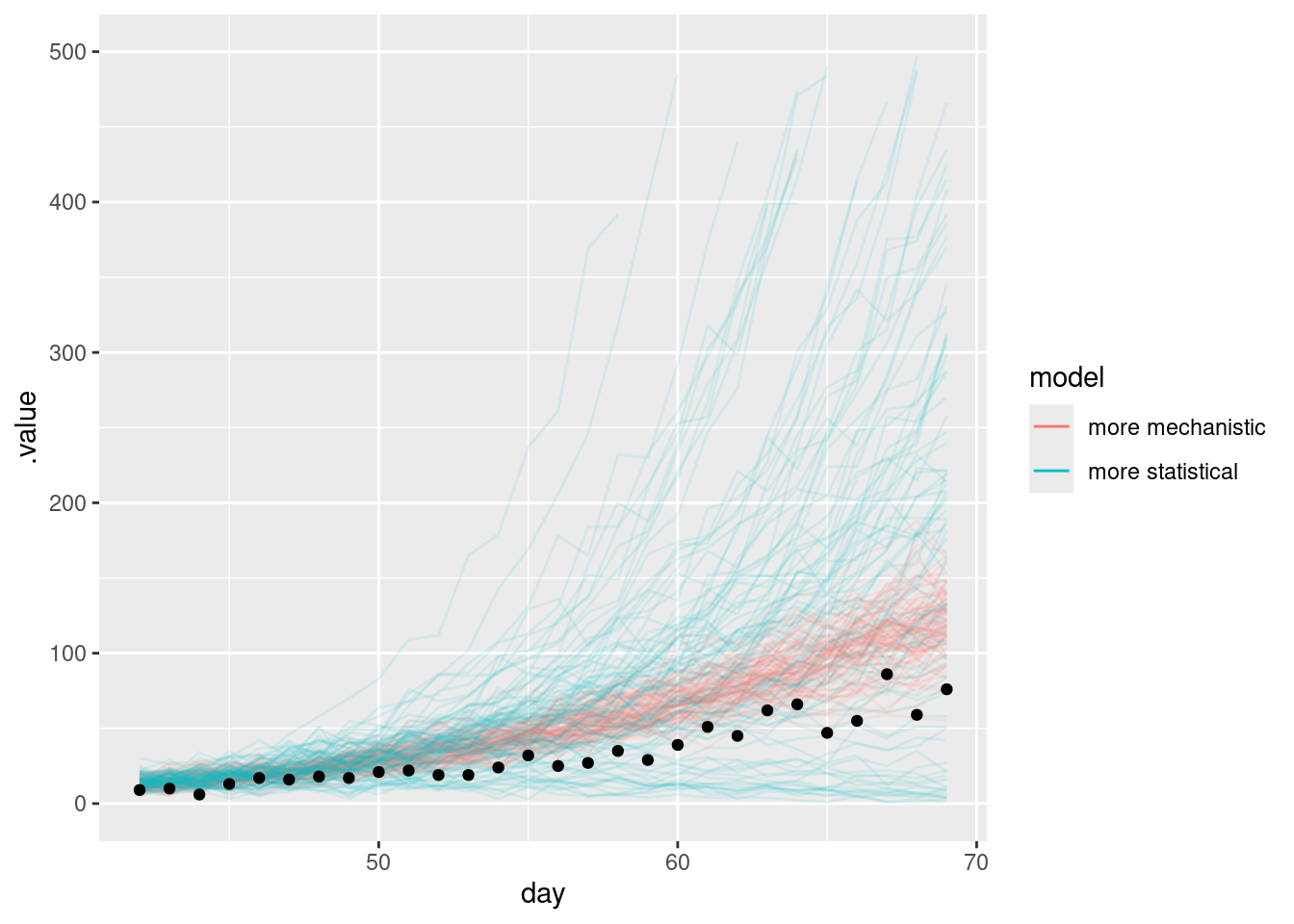
and on the log scale
forecast |>
filter(.draw %in% sample(.draw, 100)) |>
ggplot(aes(x = day)) +
geom_line(
alpha = 0.1,
aes(y = .value, group = interaction(.draw, model), colour = model)
) +
geom_point(data = target_onsets, aes(x = day, y = onsets), color = "black") +
scale_y_log10() +
guides(colour = guide_legend(override.aes = list(alpha = 1)))
Take 2 minutes
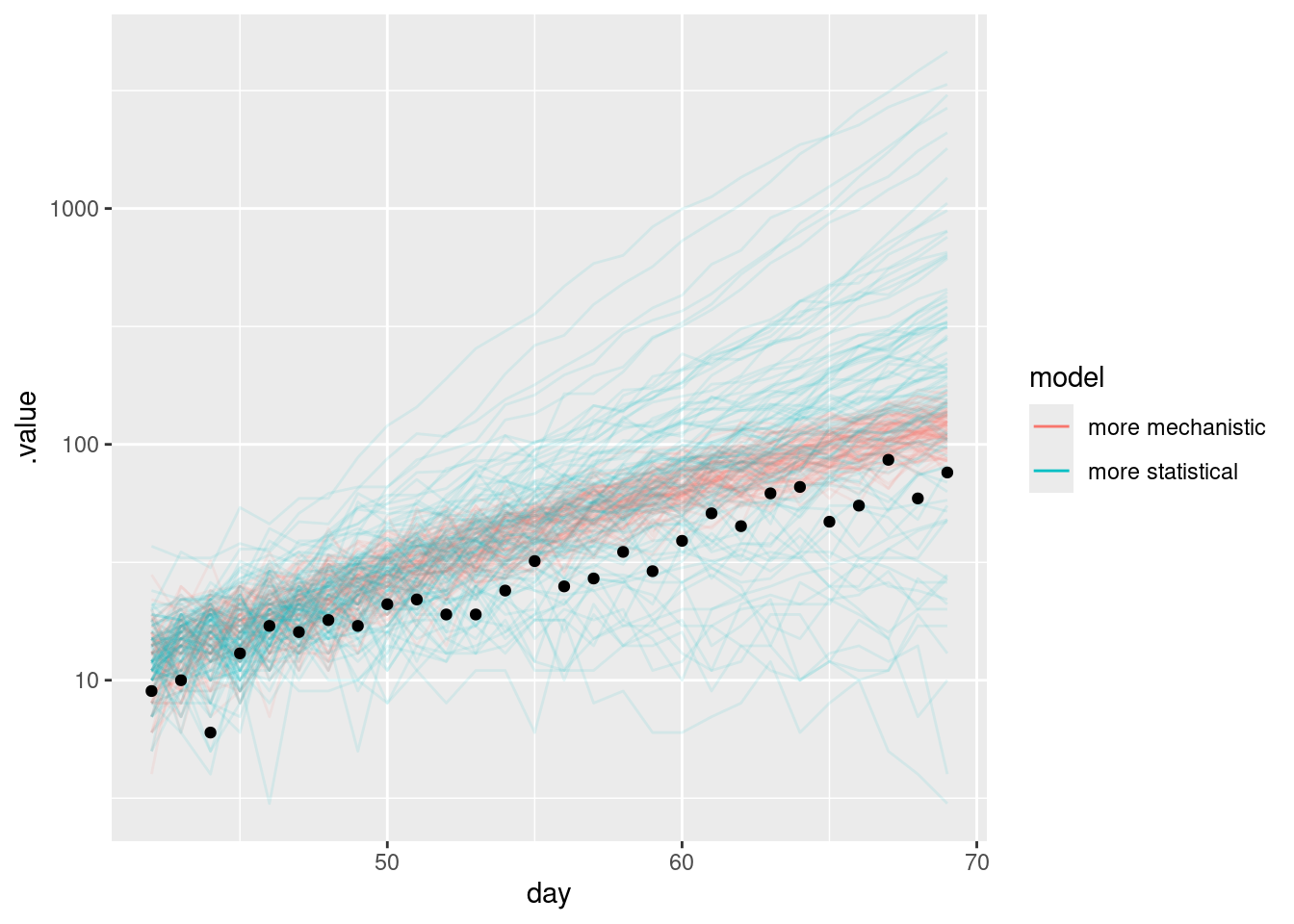
What do you notice about the forecasts from the more mechanistic and more statistical models?
Solution
- The more mechanistic model captures the downturn in the data very well.
- However it appears to be somewhat biased as it consistently overpredicts.
- The more statistical model produces some very large forecasts but also has significant probability mass on a a more rapid reduction that ultimately observed.
- Neither model simply extend the trend in the way the random walk model did in the forecasting concepts session.
Note
As these models are still renewal processes we can still plot the time-varying reproduction number which can be a helpful way of reasoning about how the models are performing.
stat_forecast_fit |>
gather_draws(R[day]) |>
ungroup() |>
filter(.draw %in% sample(.draw, 100)) |>
ggplot(aes(y = .value, x = day)) +
geom_hline(yintercept = 1, linetype = "dashed") +
geom_line(aes(group = .draw), alpha = 0.1)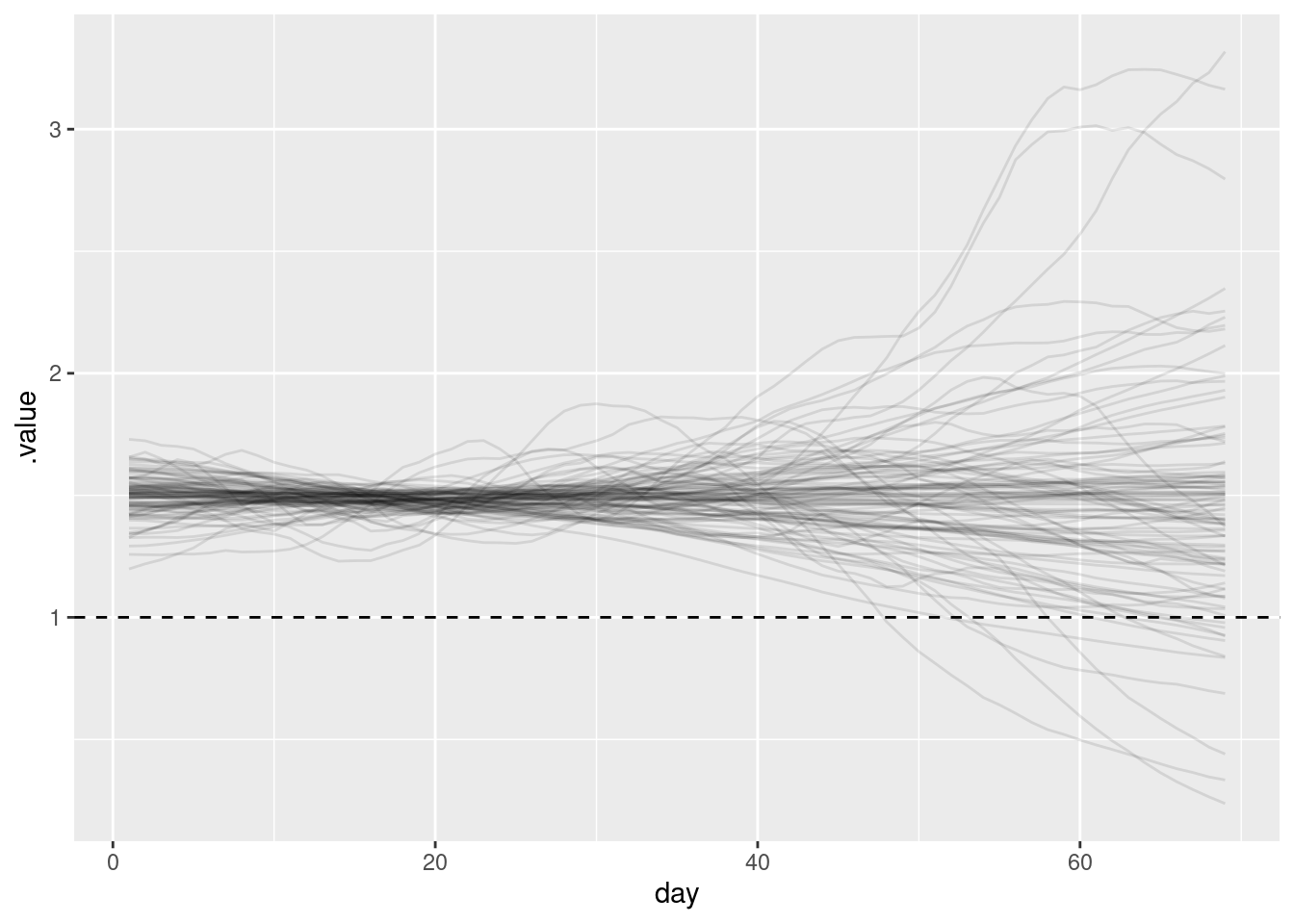
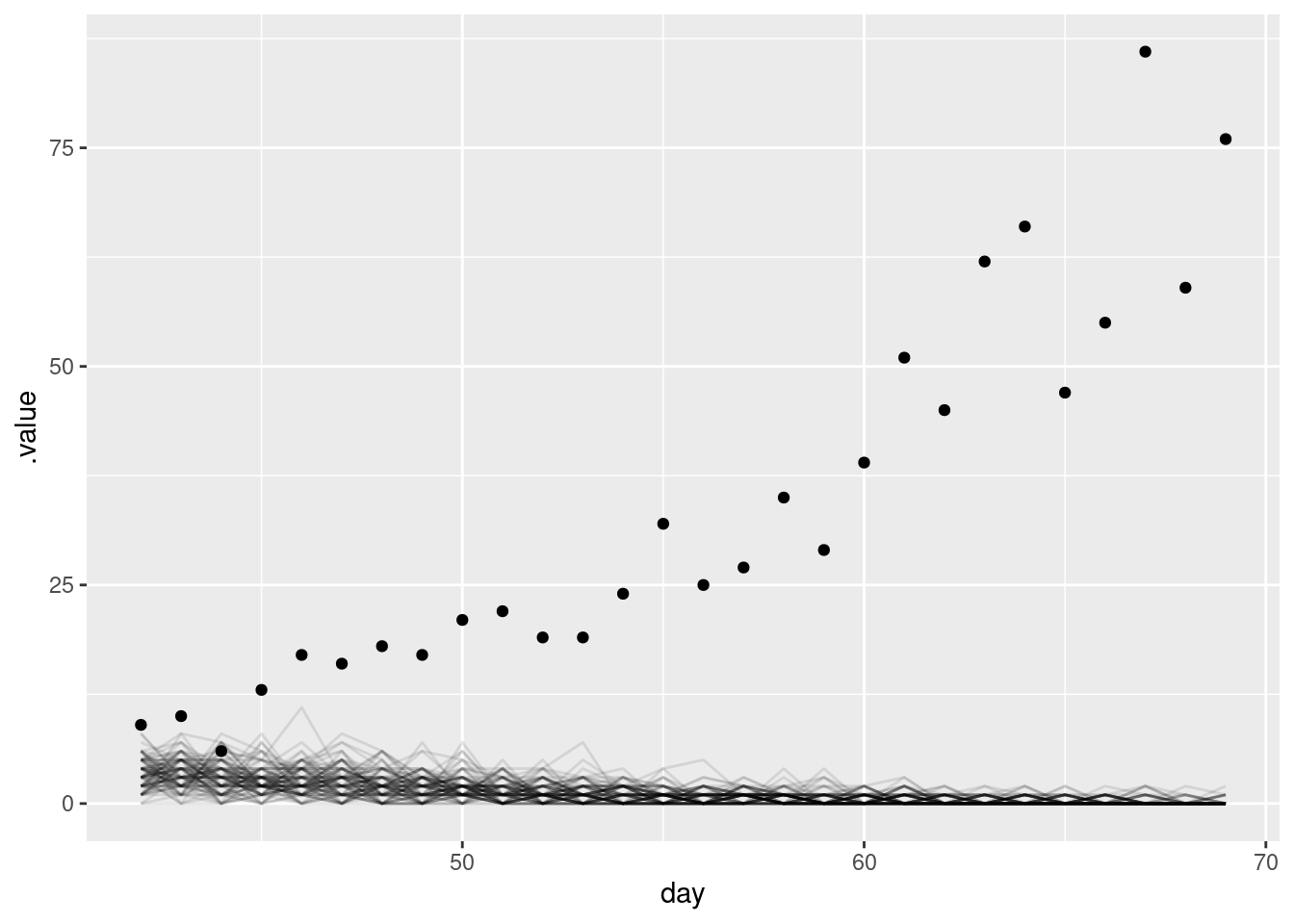
What happens when you are very wrong about the population size? (optional)
In the above we assumed that we knew the population size roughly. In practice, we may not. Refit the more mechanistic model with different priors for the population size and see how the forecasts change.
Solution
data <- list(
n = nrow(filtered_onset_df),
I0 = 1,
obs = filtered_onset_df$onsets,
gen_time_max = length(gen_time_pmf),
gen_time_pmf = gen_time_pmf,
ip_max = length(ip_pmf) - 1,
ip_pmf = ip_pmf,
h = horizon, # Here we set the number of days to forecast into the future
N_prior = c(100, 20) # the prior for the population size
)
mech_forecast_fit_diff <- mech_mod$sample(
data = data, parallel_chains = 4
)
mech_forecast_diff <- mech_forecast_fit_diff |>
gather_draws(forecast[day]) |>
ungroup() |>
mutate(day = day + cutoff)mech_forecast_diff |>
filter(.draw %in% sample(.draw, 100)) |>
ggplot(aes(y = .value, x = day)) +
geom_line(alpha = 0.1, aes(group = .draw)) +
geom_point(
data = target_onsets, aes(x = day, y = onsets),
color = "black"
)
Evaluating forecasts from our models
As in the forecasting concepts session, we have fit these models to a range of forecast dates so you don’t have to wait for the models to fit. We will now evaluate the forecasts from the mechanistic and statistical models.
data(rw_forecasts, stat_forecasts, mech_forecasts)
forecasts <- bind_rows(
rw_forecasts,
mutate(stat_forecasts, model = "More statistical"),
mutate(mech_forecasts, model = "More mechanistic")
) |>
ungroup()::: {.callout-tip, collapse=“true”} ## How did we estimate these forecasts? We generated these forecasts using the code in data-raw/generate-example-forecasts.r which uses the same approach we just took for a single forecast date but generalises it to many forecast dates.
Some important things to note about these forecasts:
- We used a 14 day forecast horizon.
- Each forecast used all the data up to the forecast date.
- We generated 1000 posterior samples for each forecast.
- We started forecasting 3 weeks into the outbreak and then forecast every 7 days until the end of the data (excluding the last 14 days to allow a full forecast).
- We use the same simulated outbreak data:
head(onset_df)# A tibble: 6 × 3
day onsets infections
<dbl> <int> <int>
1 1 0 0
2 2 0 1
3 3 0 0
4 4 0 2
5 5 0 1
6 6 0 1:::
Visualising your forecast
forecasts |>
filter(.draw %in% sample(.draw, 100)) |>
ggplot(aes(x = day)) +
geom_line(aes(y = .value, group = interaction(.draw, target_day), col = target_day), alpha = 0.1) +
geom_point(data = onset_df |>
filter(day >= 21),
aes(x = day, y = onsets), color = "black") +
scale_color_binned(type = "viridis") +
facet_wrap(~model) +
lims(y = c(0, 500))Warning: Removed 19 rows containing missing values or values outside the scale range
(`geom_line()`).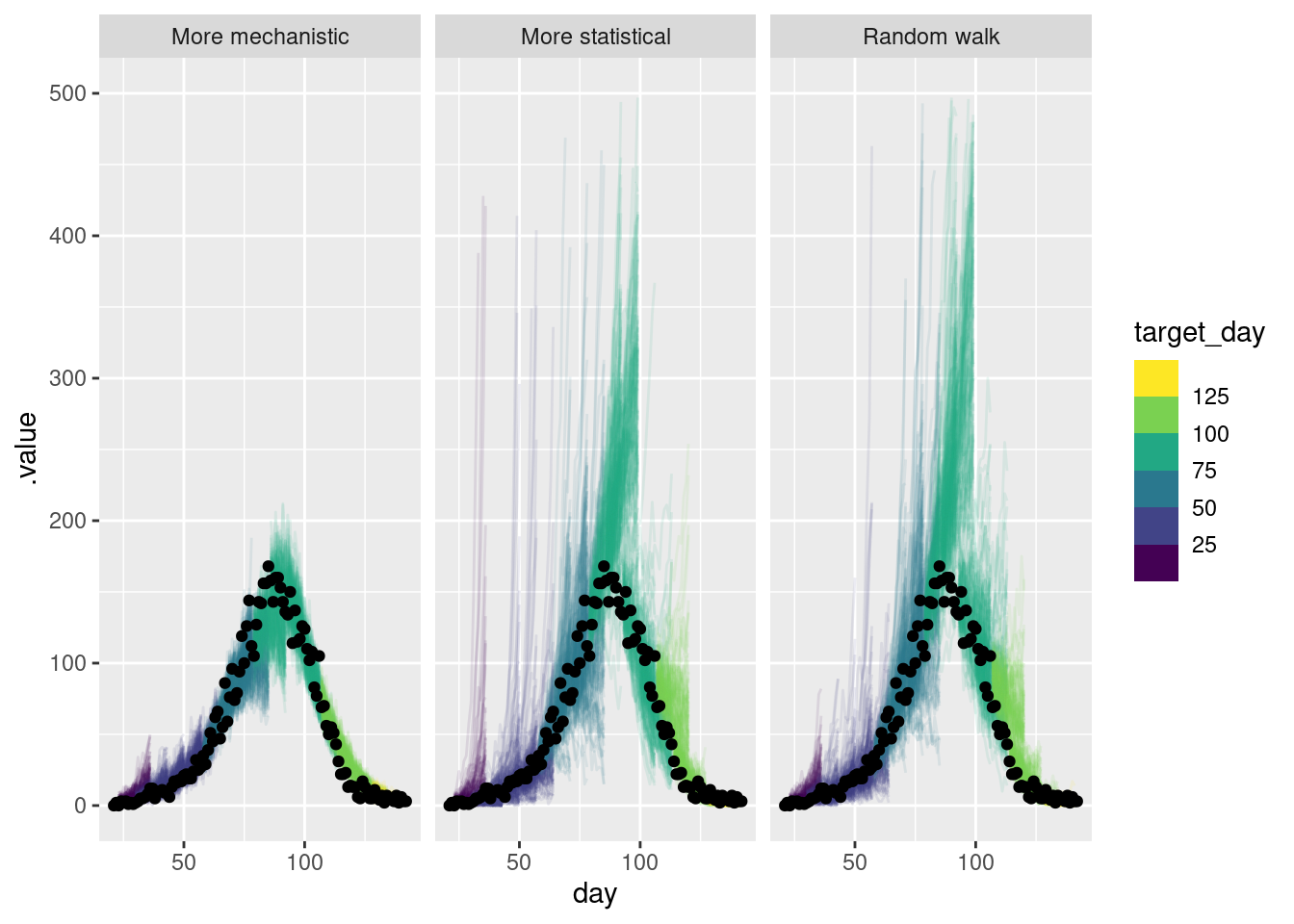
As for the single forecast it is helpful to also plot the forecast on the log scale.
forecasts |>
filter(.draw %in% sample(.draw, 100)) |>
ggplot(aes(x = day)) +
geom_line(
aes(y = .value, group = interaction(.draw, target_day), col = target_day),
alpha = 0.1
) +
geom_point(data = onset_df, aes(x = day, y = onsets), color = "black") +
scale_color_binned(type = "viridis") +
facet_wrap(~model)
Take 5 minutes
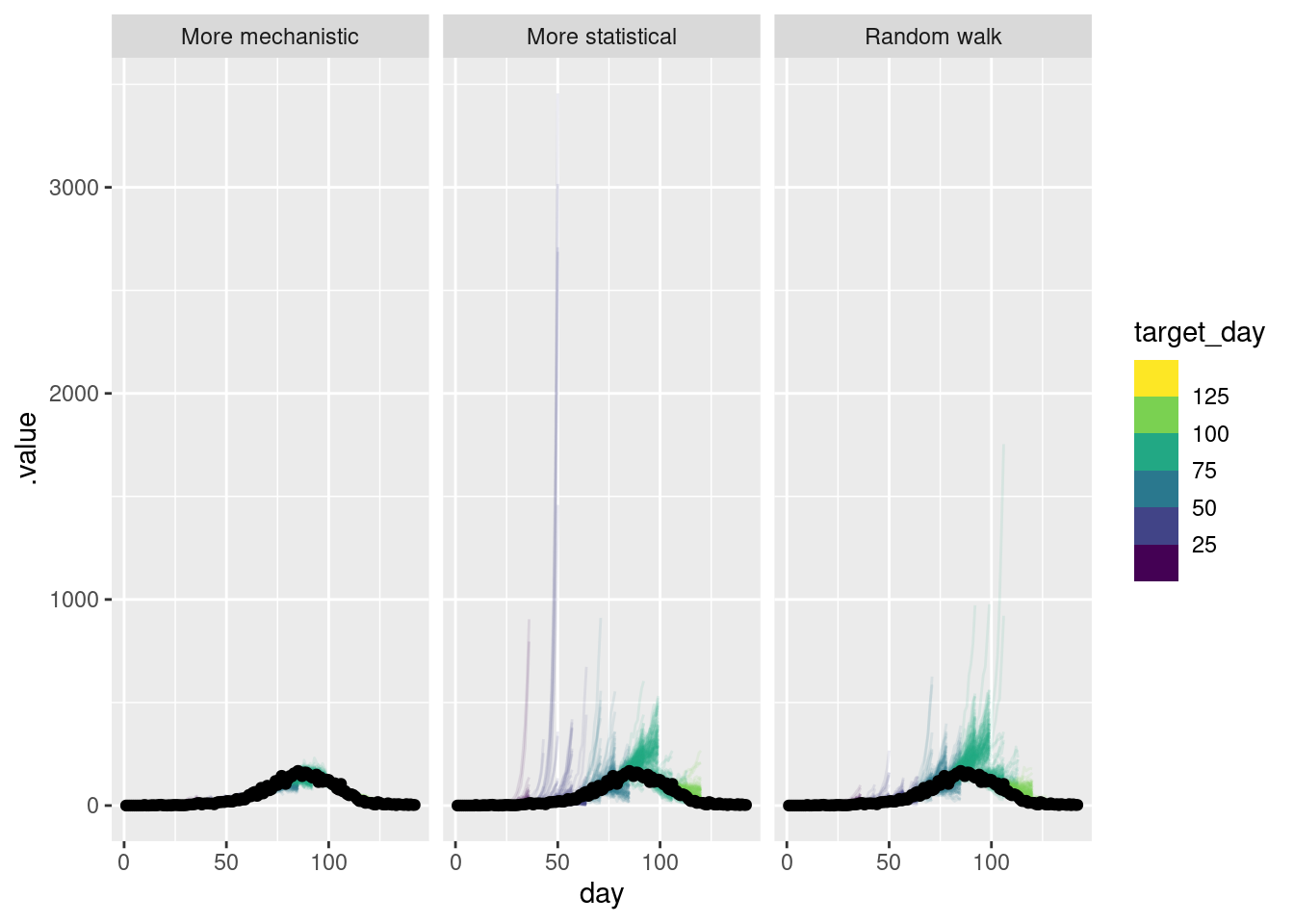
How do these forecasts compare? Which do you prefer?
Solution
How do these forecasts compare?
- The more mechanistic model captures the downturn in the data very well.
- Past the peak all models were comparable.
- The more statistical model captures the downturn faster than the random walk but less fast than the more mechanistic mode.
- The more statistical model sporadically predicts a more rapidly growing outbreak than occurred early on.
- The more statistical model is more uncertain than the mechanistic model but less uncertain than the random walk.
Which do you prefer?
- The more mechanistic model seems to be the best at capturing the downturn in the data and the uncertainty in the forecasts seems reasonable.
- If we weren’t confident in the effective susceptible population the AR model might be preferable.
Scoring your forecast
sc_forecasts <- forecasts |>
left_join(onset_df, by = "day") |>
filter(!is.na(.value)) |>
as_forecast_sample(
forecast_unit = c(
"target_day", "horizon", "model"
),
observed = "onsets",
predicted = ".value",
sample_id = ".draw"
)
sc_forecastsForecast type: sampleForecast unit:target_day, horizon, and model
sample_id predicted observed target_day horizon model
<int> <num> <int> <num> <int> <char>
1: 1 4 0 22 1 Random walk
2: 2 2 0 22 1 Random walk
3: 3 2 0 22 1 Random walk
4: 4 6 0 22 1 Random walk
5: 5 2 0 22 1 Random walk
---
671996: 996 1 3 127 14 More mechanistic
671997: 997 7 3 127 14 More mechanistic
671998: 998 2 3 127 14 More mechanistic
671999: 999 1 3 127 14 More mechanistic
672000: 1000 5 3 127 14 More mechanisticEverything seems to be in order. We can now use the scoringutils package to calculate some metrics as we did in the forecasting concepts session.
sc_scores <- sc_forecasts |>
score()
sc_scores target_day horizon model bias dss crps
<num> <int> <char> <num> <num> <num>
1: 22 1 Random walk 0.938 4.060188 2.225424
2: 22 2 Random walk 0.202 1.909537 0.552522
3: 22 3 Random walk 0.636 2.748205 1.230624
4: 22 4 Random walk 0.425 2.728959 1.002469
5: 22 5 Random walk 0.909 4.450953 3.038579
---
668: 127 10 More mechanistic 0.509 2.013433 0.809048
669: 127 11 More mechanistic -0.832 3.515779 1.970455
670: 127 12 More mechanistic 0.585 2.103694 0.918446
671: 127 13 More mechanistic -0.817 3.306240 1.802800
672: 127 14 More mechanistic -0.065 1.102604 0.371386
overprediction underprediction dispersion log_score mad ae_median
<num> <num> <num> <num> <num> <num>
1: 1.756 0.000 0.469424 2.789695 1.4826 3
2: 0.006 0.000 0.546522 1.687439 2.9652 1
3: 0.656 0.000 0.574624 2.011411 2.9652 2
4: 0.294 0.000 0.708469 2.010027 2.9652 2
5: 2.252 0.000 0.786579 2.943145 2.9652 4
---
668: 0.342 0.000 0.467048 1.802981 1.4826 1
669: 0.000 1.492 0.478455 2.551655 1.4826 3
670: 0.432 0.000 0.486446 1.848515 1.4826 1
671: 0.000 1.394 0.408800 2.611468 1.4826 3
672: 0.000 0.000 0.371386 1.333239 1.4826 0
se_mean
<num>
1: 11.519236
2: 0.831744
3: 5.654884
4: 4.190209
5: 24.157225
---
668: 2.292196
669: 8.543929
670: 2.896804
671: 7.043716
672: 0.000144scale_y_log10(limits = c(NA, 500)) + ::: {.callout-note collapse=“true”} ## Learning more about the output of score()
See the documentation for ?metrics_sample for information on the default sample metrics. :::
At a glance
Let’s summarise the scores by model first.
sc_scores |>
summarise_scores(by = "model") model bias dss crps overprediction
<char> <num> <num> <num> <num>
1: Random walk 0.23158036 6.560213 14.269480 9.100268
2: More statistical 0.05668304 6.869514 12.817473 7.035357
3: More mechanistic 0.22891518 5.772871 6.796944 2.320152
underprediction dispersion log_score mad ae_median se_mean
<num> <num> <num> <num> <num> <num>
1: 0.8166696 4.352542 4.083139 18.251203 19.05804 1662.4056
2: 1.6099732 4.172143 4.110132 17.149181 17.19643 1185.3472
3: 2.4873214 1.989470 3.810424 8.511712 9.43750 190.5546
Take 2 minutes
Before we look in detail at the scores, what do you think the scores are telling you? Which model do you think is best?
Continuous ranked probability score
As in the forecasting concepts session, we will start by looking at the CRPS by horizon and forecast date.
Reminder: Key things to note about the CRPS
- Small values are better
- As it is an absolute scoring rule it can be difficult to use to compare forecasts across scales.
First by forecast horizon.
sc_scores |>
summarise_scores(by = c("model", "horizon")) |>
ggplot(aes(x = horizon, y = crps, col = model)) +
geom_point()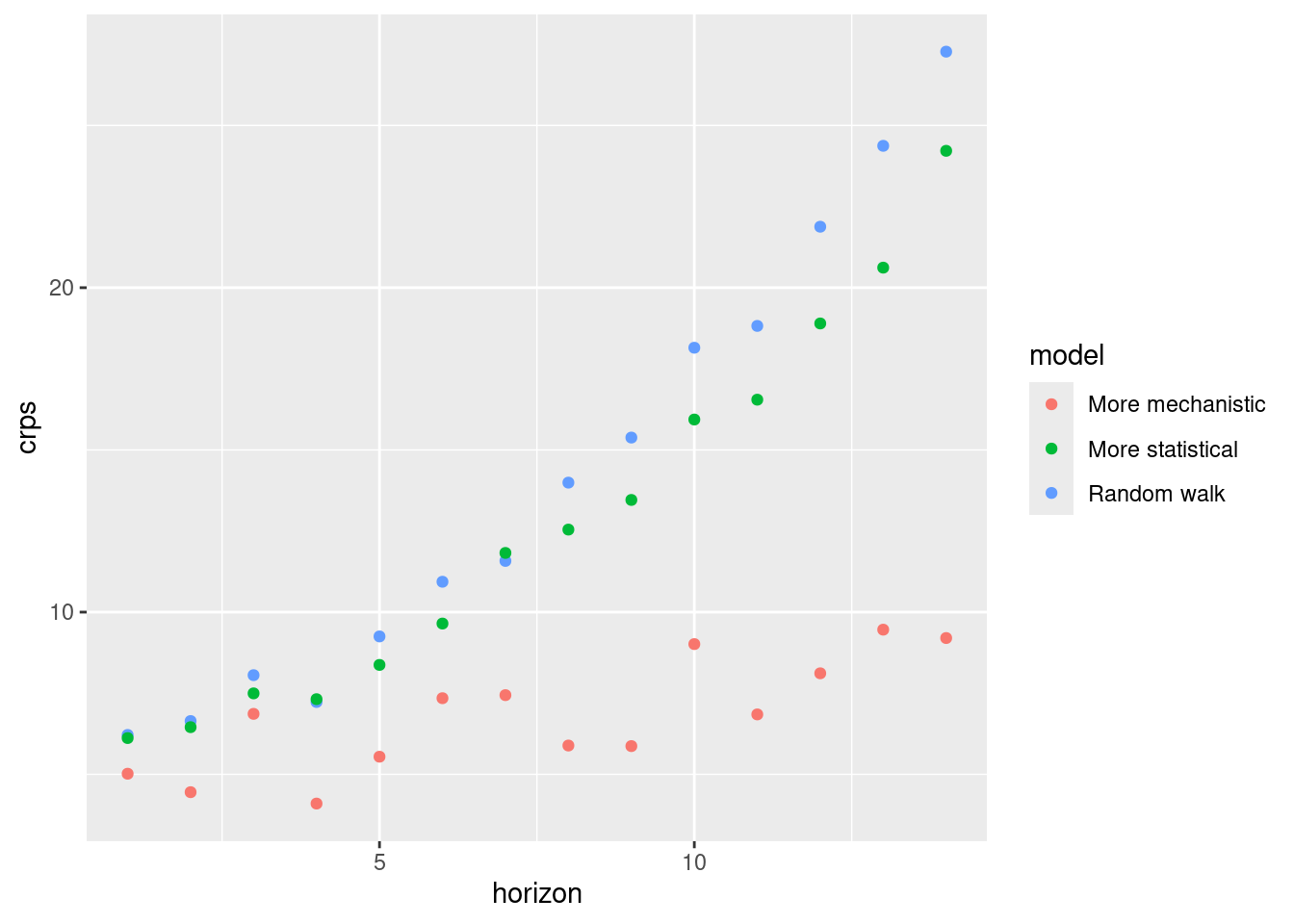
and across different forecast dates
sc_scores |>
summarise_scores(by = c("target_day", "model")) |>
ggplot(aes(x = target_day, y = crps, col = model)) +
geom_point()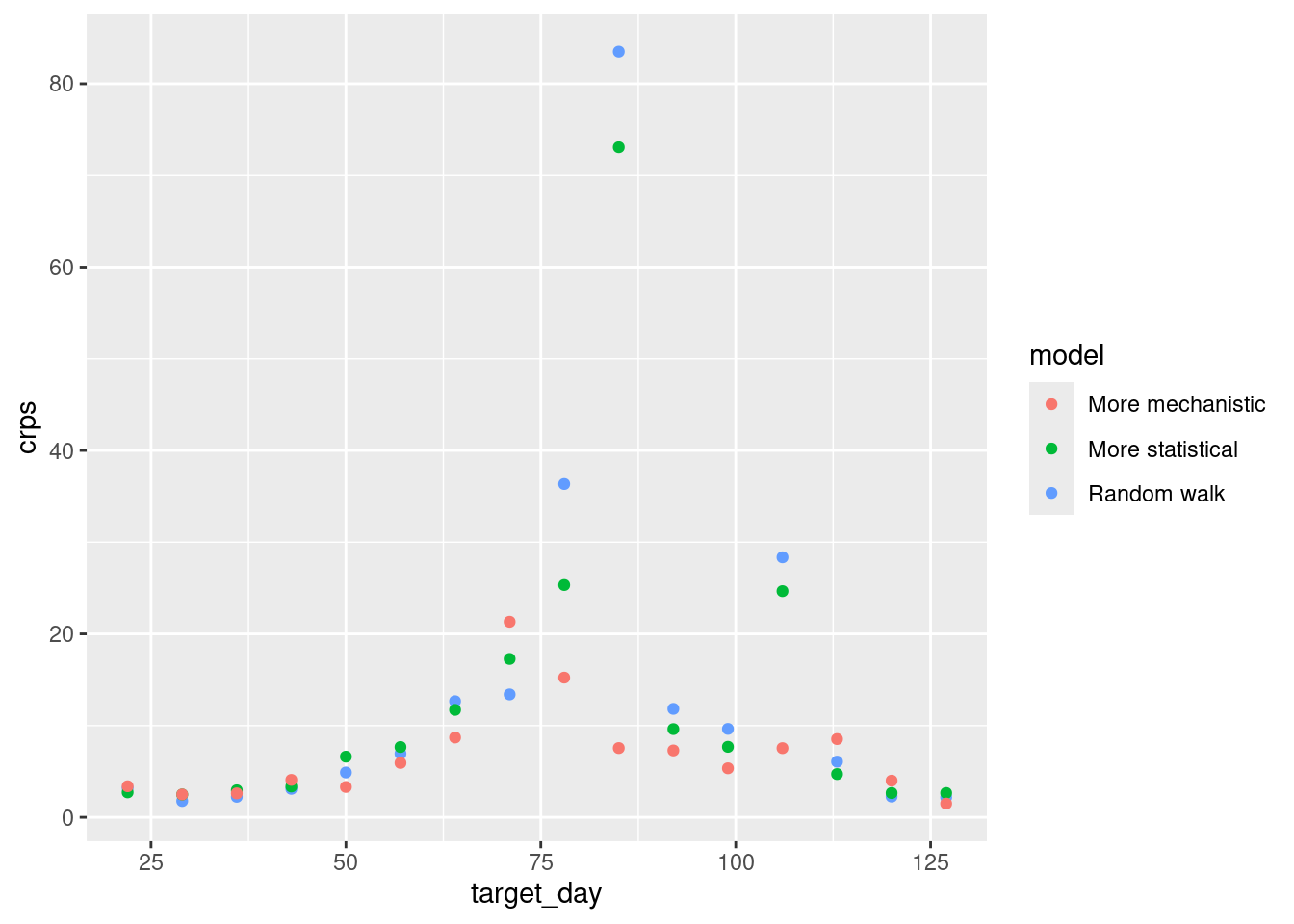
Take 5 minutes
How do the CRPS scores change based on forecast date? How do the CRPS scores change with forecast horizon?
Solution
How do the CRPS scores change based on forecast horizon?
- All models have increasing CRPS with forecast horizon.
- The more mechanistic model has the lowest CRPS at all forecast horizon.
- The more stastical model starts to outperform the random walk model at longer time horizons.
How do the CRPS scores change with forecast date?
- The more statistical model does particularly poorly around the peak of the outbreak but outperforms the random walk model.
- The more mechanistic model does particularly well around the peak of the outbreak versus all other models
- The more statistical model starts to outperfrom the other models towards the end of the outbreak.
PIT histograms
Reminder: Interpreting the PIT histogram
- Ideally PIT histograms should be uniform.
- If is a U shape then the model is overconfident and if it is an inverted U shape then the model is underconfident.
- If it is skewed then the model is biased towards the direction of the skew.
Let’s first look at the overall PIT histogram.
sc_forecasts |>
get_pit_histogram(by = "model") |>
ggplot(aes(x = mid, y = density)) +
geom_col() +
facet_wrap(~model)
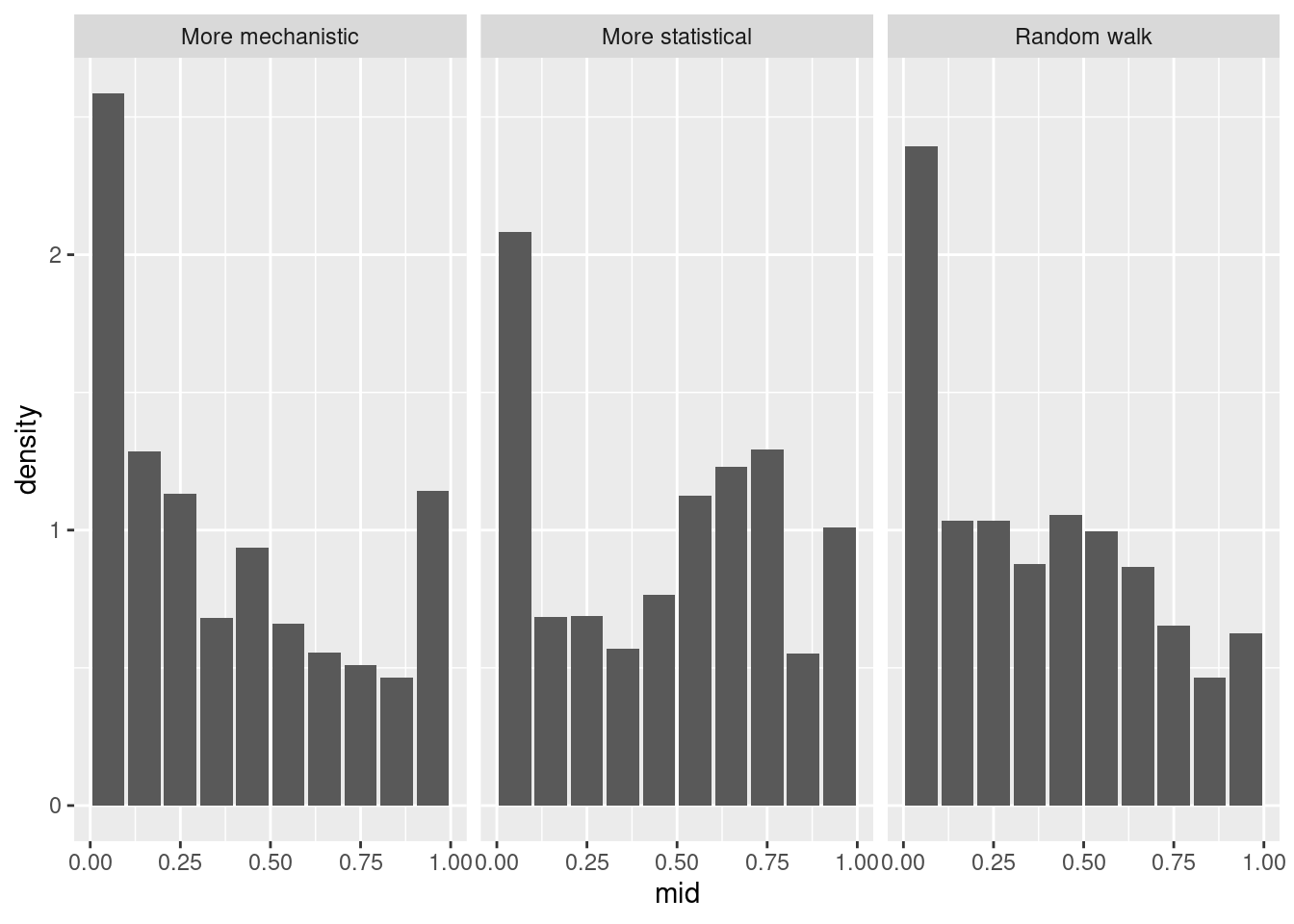
As before let’s look at the PIT histogram by forecast horizon (to save space we will group horizons)
sc_forecasts |>
mutate(group_horizon = case_when(
horizon <= 3 ~ "1-3",
horizon <= 7 ~ "4-7",
horizon <= 14 ~ "8-14"
)) |>
get_pit_histogram(by = c("model", "group_horizon")) |>
ggplot(aes(x = mid, y = density)) +
geom_col() +
facet_grid(vars(model), vars(group_horizon))
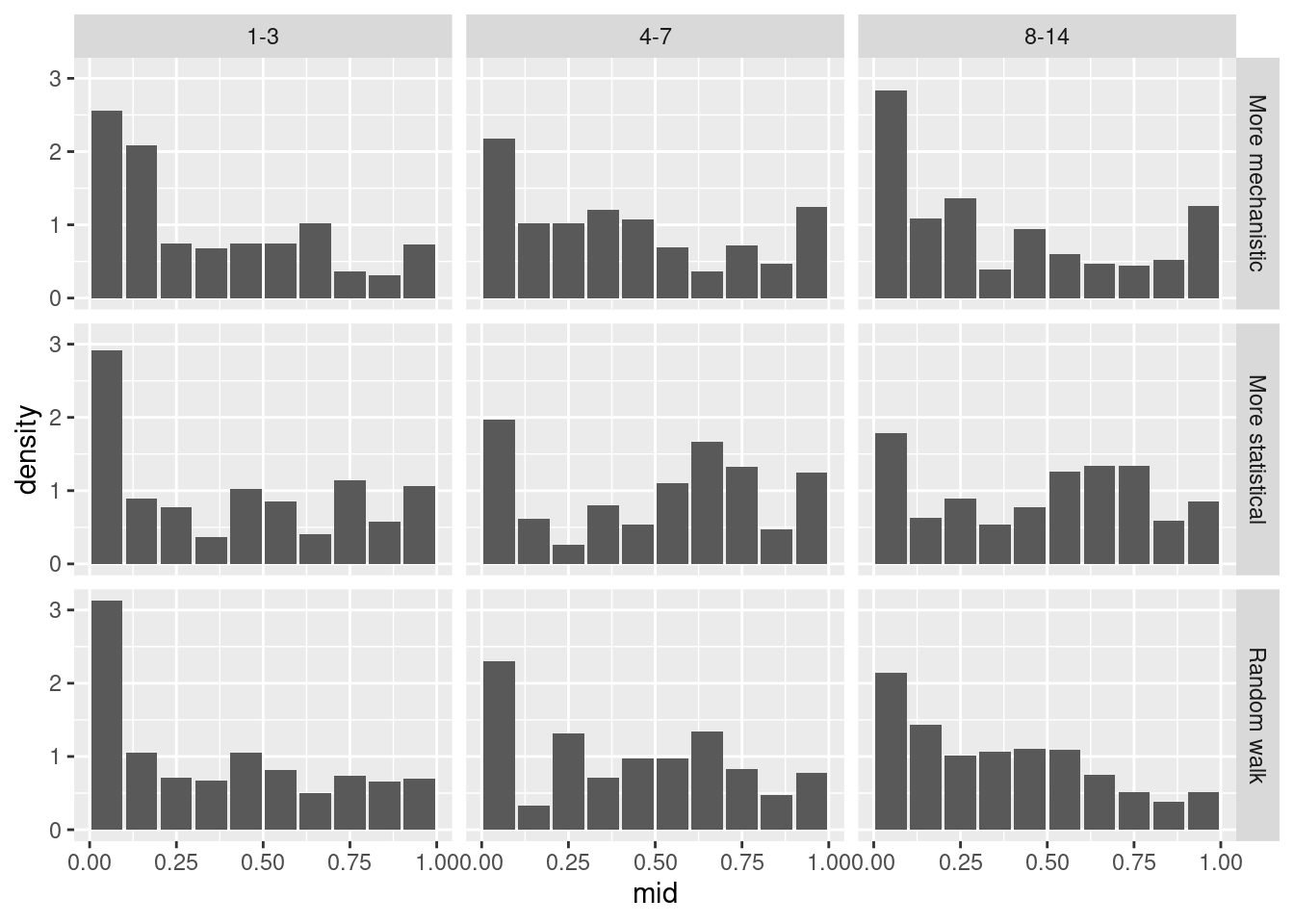
and then for different forecast dates.
sc_forecasts |>
get_pit_histogram(by = c("model", "target_day")) |>
ggplot(aes(x = mid, y = density)) +
geom_col() +
facet_grid(vars(model), vars(target_day))
Take 5 minutes
What do you think of the PIT histograms?
Solution
What do you think of the PIT histograms?
- The more mechanistic model is reasonably well calibrated but has a slight tendency to be overconfident.
- The random walk is biased towards overpredicting.
- The more statistical model is underconfident.
- Across horizons the more mechanistic model is only liable to underpredict at the longest horizons.
- The random walk model is initially relatively unbiased and well calibrated but becomes increasingly likely to overpredict as the horizon increases.
- The forecast date stratified PIT histograms are hard to interpret. We may need to find other ways to visualise bias and calibration at this level of stratification (see the
{scoringutils}documentation for some ideas).
Scoring on the log scale
Again as in the forecasting concepts session, we will also score the forecasts on the log scale.
log_sc_forecasts <- sc_forecasts |>
transform_forecasts(
fun = log_shift,
offset = 1,
append = FALSE
)
log_sc_scores <- log_sc_forecasts |>
score()
Tip
Reminder: For more on scoring on the log scale see this paper on scoring forecasts on transformed scales.
At a glance
log_sc_scores |>
summarise_scores(by = "model") model bias dss crps overprediction
<char> <num> <num> <num> <num>
1: Random walk 0.19532143 -0.2881110 0.2604827 0.1345397
2: More statistical 0.02349107 -0.1955428 0.2749484 0.1010849
3: More mechanistic 0.18734821 -0.7400627 0.2067305 0.1311370
underprediction dispersion log_score mad ae_median se_mean
<num> <num> <num> <num> <num> <num>
1: 0.03883240 0.08711065 0.6859391 0.3761217 0.3446957 0.2296360
2: 0.07286781 0.10099568 0.7216743 0.4197095 0.3692371 0.2544433
3: 0.02400668 0.05158679 0.5900611 0.2182572 0.2806367 0.1539763
Take 2 minutes
Before we look in detail at the scores, what do you think the scores are telling you? Which model do you think is best?
CRPS
log_sc_scores |>
summarise_scores(by = c("model", "horizon")) |>
ggplot(aes(x = horizon, y = crps, col = model)) +
geom_point()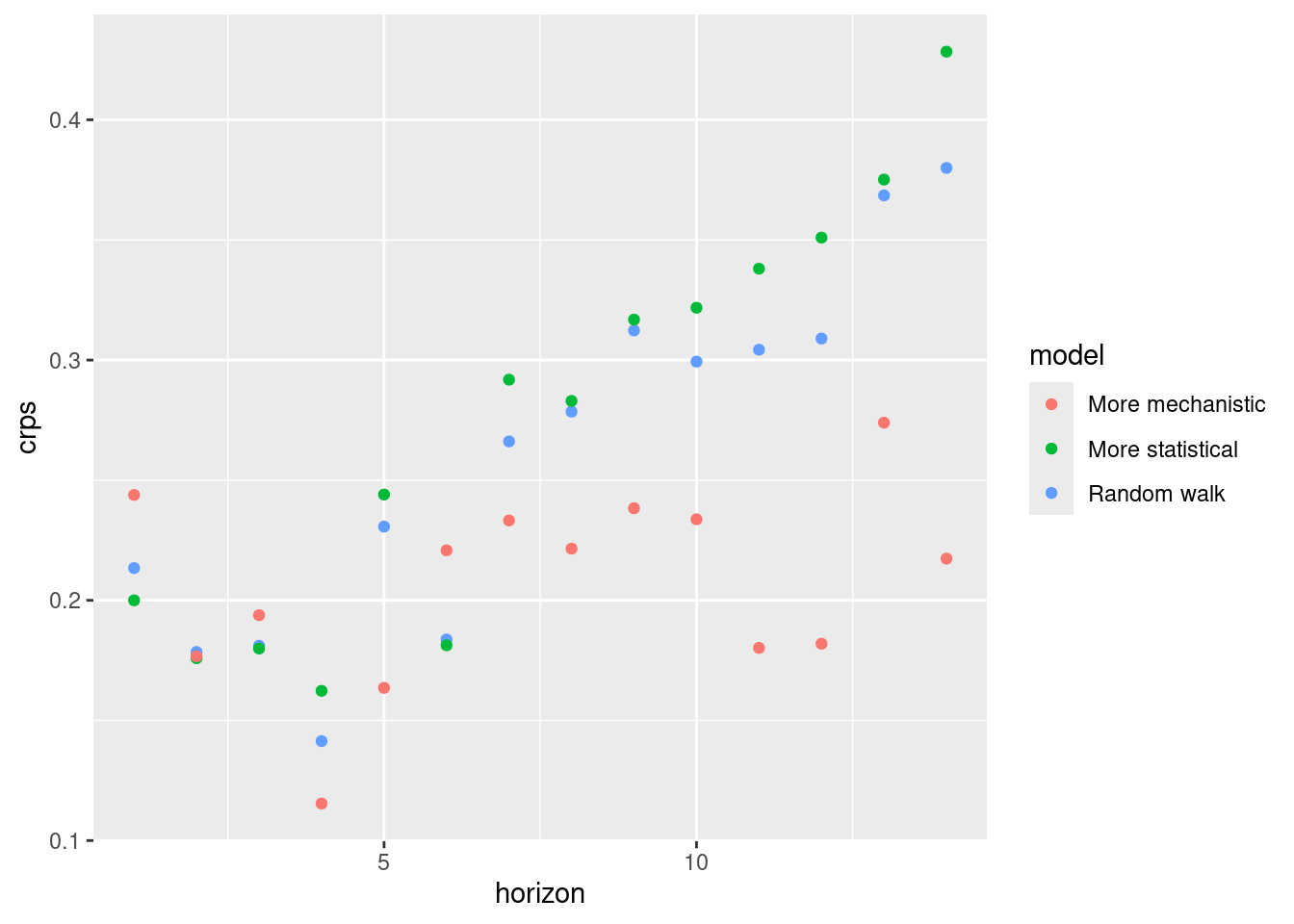
log_sc_scores |>
summarise_scores(by = c("target_day", "model")) |>
ggplot(aes(x = target_day, y = crps, col = model)) +
geom_point()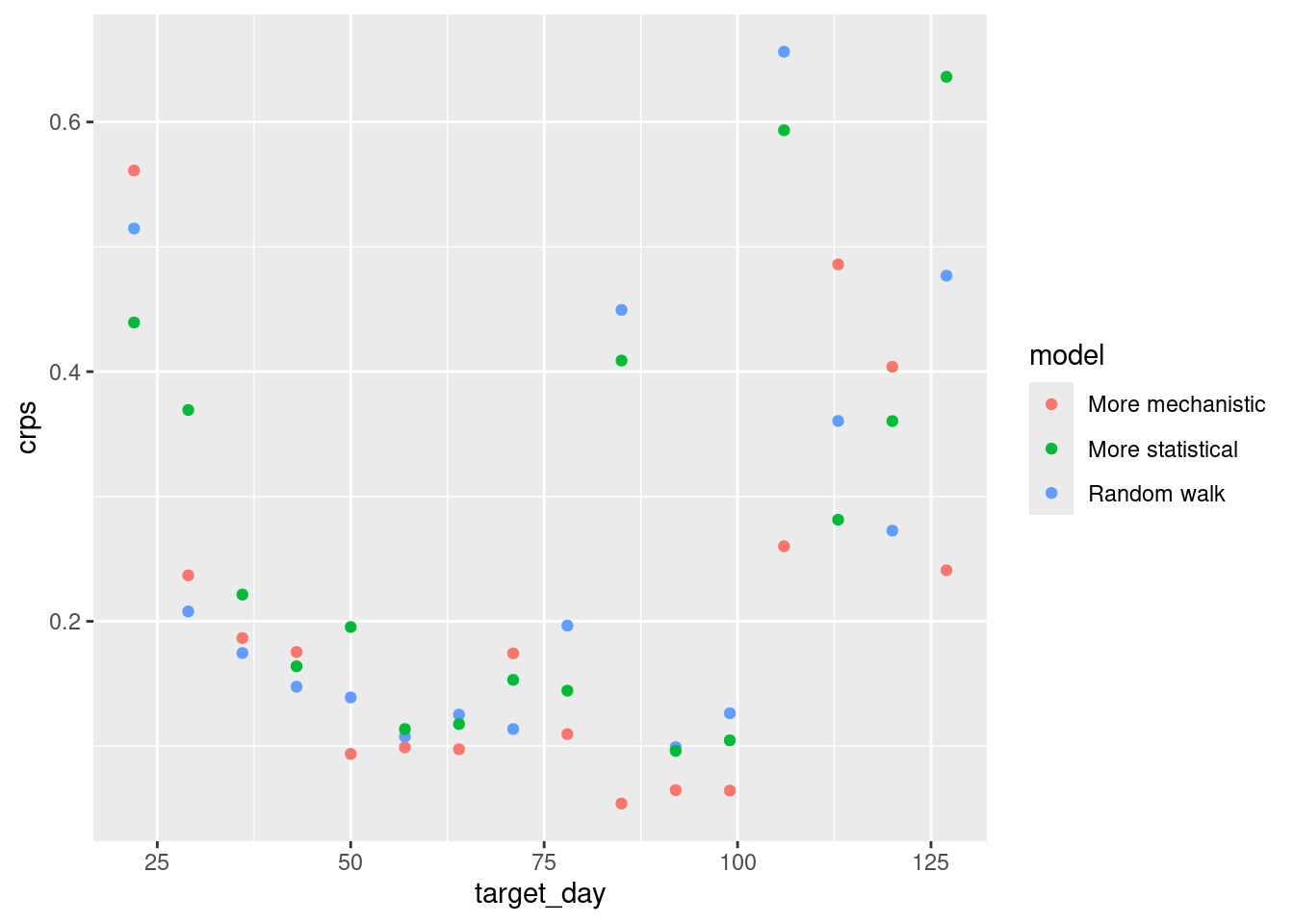
Take 5 minutes
How do the CRPS scores on the log scale compare to the scores on the original scale?
Solution
- The performance of the mechanistic model is more variable across forecast horizon than on the natural scale.
- On the log scale the by horizon performance of the random walk and more statistical mdoel is more comparable than on the log scale.
- The period of high incidence dominates the target day stratified scores less on the log scale. We see that all models performed less well early and late on.
PIT histograms
log_sc_forecasts |>
get_pit_histogram(by = "model") |>
ggplot(aes(x = mid, y = density)) +
geom_col() +
facet_wrap(~model)
log_sc_forecasts |>
mutate(group_horizon = case_when(
horizon <= 3 ~ "1-3",
horizon <= 7 ~ "4-7",
horizon <= 14 ~ "8-14"
)) |>
get_pit_histogram(by = c("model", "group_horizon")) |>
ggplot(aes(x = mid, y = density)) +
geom_col() +
facet_grid(vars(model), vars(group_horizon))
log_sc_forecasts |>
get_pit_histogram(by = c("model", "target_day")) |>
ggplot(aes(x = mid, y = density)) +
geom_col() +
facet_grid(vars(model), vars(target_day))
Take 5 minutes
What do you think of the PIT histograms?
Solution
The PIT histograms are similar to the original scale PIT histograms but the mechanistic model appears better calibrated.
Going further
- We have only looked at three forecasting models here. There are many more models that could be used. For example, we could use a more complex mechanistic model which captures more of the underlying dynamics of the data generating process. We could also use a more complex statistical model which captures more of the underlying structure of the data.
- We could also combine the more mechanistic and more statistical models to create a hybrid model which captures the best of both worlds (maybe).
- We could also use a more complex scoring rule to evaluate the forecasts. For example, we could use a multivariate scoring rule which captures more of the structure of the data.