Evaluating real-world outbreak forecasts

Introduction

So far in this course we have focused on building, visualising, evaluating, and combining “toy” forecast models in somewhat synthetic settings. In this session you will work with real forecasts from an existing modeling hub. This will expose many of the challenges involved with real-time forecasting, as well as the benefits of coordinated modeling efforts.

Slides

Real-world forecasts

Objectives

The aim of this session is to develop advanced skills in working with real forecasts and an appreciation for the challenges of real-time forecasting.

Setup

Source file

The source file of this session is located at sessions/real-world-forecasts.qmd.

Libraries used

In this session we will use the nfidd package to access some stored datasets, the dplyr package for data wrangling, the ggplot2 library for plotting, and the following hubverse packages: hubData, hubUtils, hubEvals and hubEnsembles.

library("nfidd")
library("dplyr")
library("ggplot2")
library("hubData")
library("hubUtils")
library("hubEvals")
library("hubEnsembles")
theme_set(theme_bw())

Tip

The best way to interact with the material is via the Visual Editor of RStudio.

Initialisation

We set a random seed for reproducibility. Setting this ensures that you should get exactly the same results on your computer as we do. This is not strictly necessary but will help us talk about the models.

set.seed(5050) # for Shohei Ohtani!

Introduction to the US COVID-19 Forecast Hub

The US COVID-19 Forecast Hub is a collaborative epidemiological forecasting project that started in April 2020. From 2020 through summer 2024, the project was hosted by the Reich Lab at UMass-Amherst. The short-term forecasts were published on the US CDC website as the official forecasts of record from the federal government.

During this time, the project collected over 9,000 forecast submissions from 130 models. The project collected nearly 1 billion rows of model output data, and has led to multiple research papers on epidemiological forecasting.(Ray et al. 2023; Cramer et al. 2022; Fox et al. 2024; Kim, Ray, and Reich 2024)

The project paused forecasting during the 2024 summer, and restarted in late fall 2024 under the purview of the US CDC Centers for Forecasting and Outbreak Analytics (CFA). When it re-started, the hub was launched using hubverse-style forecast guidelines. The public dashboard for the COVID-19 Forecast Hub has an up-to-date record of the forecasts submitted.

In this session, we will access and analyse forecasts from the CFA-run US COVID-19 Forecast Hub.

Take 5 minutes

Browse the current US COVID-19 Forecast Hub Dashboard. Write down three observations that are interesting or surprising to you. Share them with your neighbor(s) and listen to their observations.

Forecast dimensions

Here are some details about the structure of the COVID-19 Forecast Hub project.

Forecasts are collected every week, with submissions due on Wednesdays.
Teams make predictions of -1 through 3 week ahead counts of new hospital admissions due to COVID-19.
The ground truth data (“target data” in hubverse lingo) is taken from the Weekly Hospital Respiratory Data (HRD) Metrics by Jurisdiction, National Healthcare Safety Network (NHSN) dataset.
Teams may forecast for up to 53 locations, including the US national level, all 50 states, plus Puerto Rico and Washington DC.
Forecasts are solicited in a quantile format.

Further details about the hub are available at its GitHub README page.

The forecasts

We will start by accessing forecast data from the COVID-19 Forecast Hub. Because the hub takes advantage of hubverse cloud data storage architecture, both the forecast and target data are stored in an S3 bucket that can be accessed using the hubData R package.

Tip

For a complete list of hubs (many of which have public data available) check out the hubverse list of hubs.

Accessing forecast data from the cloud

The following code can be used to retrieve covid forecasts from the cloud. However, there are over 2 million rows of data, and it can take some bandwidth to download. To make these results more reproducible and to provide a snapshot of the data, we also provide the forecasts as a data object that can be loaded directly from the nfidd package.

hub_path_cloud <- hubData::s3_bucket("s3://covid19-forecast-hub")
hub_con_cloud <- hubData::connect_hub(hub_path_cloud, skip_checks = TRUE)

data(covid_locations)

covid_forecasts <- hub_con_cloud |> 
  filter(
    output_type == "quantile",
    target == "wk inc covid hosp",
    horizon >= 0
    ) |> 
  collect() |> 
  left_join(covid_locations)

This line of code will load all the forecasts saved in the package into your R session.

data(covid_forecasts)

Accessing target data from the cloud

Here is code to query the time-series data from the cloud-based hub.

covid_time_series <- connect_target_timeseries(hub_path_cloud) |> 
  filter(target == "wk inc covid hosp") |> 
  collect() |> 
  left_join(covid_locations)

However, to ensure reproducibility (since this is a live dataset), we have downloaded this object for you already as of July 9, 2025, and it is available to load in from the course R package directly.

data(covid_time_series)

Exploratory data analysis and visualization

Now that we’ve downloaded the forecast and target data, let’s just do a few basic explorations to make sure we understand the dimensions of our data. Ideally, storing data in the hubverse ensures that the data is “clean”, no typos in targets or locations, no missing quantile levels, no negative predictions, etc… But let’s start by just getting a sense of how many unique values we have for location, horizon, target_end_date, etc…

unique_per_column <- covid_forecasts  |> 
  select(-value) |> 
  purrr::map(~ sort(unique(.x)))
unique_per_column

$reference_date
 [1] "2024-11-23" "2024-11-30" "2024-12-07" "2024-12-14" "2024-12-21"
 [6] "2024-12-28" "2025-01-04" "2025-01-11" "2025-01-18" "2025-01-25"
[11] "2025-02-01" "2025-02-08" "2025-02-15" "2025-02-22" "2025-03-01"
[16] "2025-03-08" "2025-03-15" "2025-03-22" "2025-03-29" "2025-04-05"
[21] "2025-04-12" "2025-04-19" "2025-04-26" "2025-05-03" "2025-05-10"
[26] "2025-05-17" "2025-05-24" "2025-05-31" "2025-06-07" "2025-06-14"
[31] "2025-06-21" "2025-06-28" "2025-07-05" "2025-07-12"

$location
 [1] "01" "02" "04" "05" "06" "08" "09" "10" "11" "12" "13" "15" "16" "17" "18"
[16] "19" "20" "21" "22" "23" "24" "25" "26" "27" "28" "29" "30" "31" "32" "33"
[31] "34" "35" "36" "37" "38" "39" "40" "41" "42" "44" "45" "46" "47" "48" "49"
[46] "50" "51" "53" "54" "55" "56" "72" "US"

$horizon
[1] 0 1 2 3

$target_end_date
 [1] "2024-11-23" "2024-11-30" "2024-12-07" "2024-12-14" "2024-12-21"
 [6] "2024-12-28" "2025-01-04" "2025-01-11" "2025-01-18" "2025-01-25"
[11] "2025-02-01" "2025-02-08" "2025-02-15" "2025-02-22" "2025-03-01"
[16] "2025-03-08" "2025-03-15" "2025-03-22" "2025-03-29" "2025-04-05"
[21] "2025-04-12" "2025-04-19" "2025-04-26" "2025-05-03" "2025-05-10"
[26] "2025-05-17" "2025-05-24" "2025-05-31" "2025-06-07" "2025-06-14"
[31] "2025-06-21" "2025-06-28" "2025-07-05" "2025-07-12" "2025-07-19"
[36] "2025-07-26" "2025-08-02"

$target
[1] "wk inc covid hosp"

$output_type
[1] "quantile"

$output_type_id
 [1] "0.01"  "0.025" "0.05"  "0.1"   "0.15"  "0.2"   "0.25"  "0.3"   "0.35" 
[10] "0.4"   "0.45"  "0.5"   "0.55"  "0.6"   "0.65"  "0.7"   "0.75"  "0.8"  
[19] "0.85"  "0.9"   "0.95"  "0.975" "0.99" 

$model_id
 [1] "CEPH-Rtrend_covid"            "CFA_Pyrenew-Pyrenew_H_COVID" 
 [3] "CFA_Pyrenew-Pyrenew_HE_COVID" "CFA_Pyrenew-Pyrenew_HW_COVID"
 [5] "CFA_Pyrenew-PyrenewHEW_COVID" "CMU-climate_baseline"        
 [7] "CMU-TimeSeries"               "CovidHub-baseline"           
 [9] "CovidHub-ensemble"            "Google_SAI-Ensemble"         
[11] "JHU_CSSE-CSSE_Ensemble"       "Metaculus-cp"                
[13] "MOBS-GLEAM_COVID"             "NEU_ISI-AdaptiveEnsemble"    
[15] "OHT_JHU-nbxd"                 "UGA_flucast-INFLAenza"       
[17] "UM-DeepOutbreak"              "UMass-ar6_pooled"            
[19] "UMass-gbqr"                  

$abbreviation
 [1] "AK" "AL" "AR" "AZ" "CA" "CO" "CT" "DC" "DE" "FL" "GA" "HI" "IA" "ID" "IL"
[16] "IN" "KS" "KY" "LA" "MA" "MD" "ME" "MI" "MN" "MO" "MS" "MT" "NC" "ND" "NE"
[31] "NH" "NJ" "NM" "NV" "NY" "OH" "OK" "OR" "PA" "PR" "RI" "SC" "SD" "TN" "TX"
[46] "US" "UT" "VA" "VT" "WA" "WI" "WV" "WY"

$location_name
 [1] "Alabama"              "Alaska"               "Arizona"             
 [4] "Arkansas"             "California"           "Colorado"            
 [7] "Connecticut"          "Delaware"             "District of Columbia"
[10] "Florida"              "Georgia"              "Hawaii"              
[13] "Idaho"                "Illinois"             "Indiana"             
[16] "Iowa"                 "Kansas"               "Kentucky"            
[19] "Louisiana"            "Maine"                "Maryland"            
[22] "Massachusetts"        "Michigan"             "Minnesota"           
[25] "Mississippi"          "Missouri"             "Montana"             
[28] "Nebraska"             "Nevada"               "New Hampshire"       
[31] "New Jersey"           "New Mexico"           "New York"            
[34] "North Carolina"       "North Dakota"         "Ohio"                
[37] "Oklahoma"             "Oregon"               "Pennsylvania"        
[40] "Puerto Rico"          "Rhode Island"         "South Carolina"      
[43] "South Dakota"         "Tennessee"            "Texas"               
[46] "US"                   "Utah"                 "Vermont"             
[49] "Virginia"             "Washington"           "West Virginia"       
[52] "Wisconsin"            "Wyoming"             

$population
 [1]    578759    623989    705749    731545    762062    884659    973764
 [8]   1059361   1068778   1344212   1359711   1415872   1787065   1792147
[15]   1934408   2096829   2913314   2976149   3017804   3080156   3155070
[22]   3205958   3565287   3754939   3956971   4217737   4467673   4648794
[29]   4903185   5148714   5639632   5758736   5822434   6045680   6626371
[36]   6732219   6829174   6892503   7278717   7614893   8535519   8882190
[43]   9986857  10488084  10617423  11689100  12671821  12801989  19453561
[50]  21477737  28995881  39512223 332875137

From the above, we can see that

the forecasts were made every week from 2024-11-23 until 2025-07-12,
there is just one target, the weekly counts of hospital admissions due to COVID-19, and we only have quantile values for it,
we have forecasts for horizons 0 to 3 weeks,
there are 23 quantile levels present in the data,
there are 19 models.

Let’s just do a quick visualization of forecasts from one week to make sure we understand the structure of what one date and location’s worth of forecasts look like.

covid_forecasts |> 
  filter(reference_date == "2025-02-15", abbreviation == "GA") |> 
  hubVis::plot_step_ahead_model_output(
    target_data = covid_time_series |> 
      filter(as_of == as.Date("2025-07-09"),
             abbreviation == "GA"),
    use_median_as_point = TRUE,
    x_col_name = "target_end_date",
    x_target_col_name = "date",
    pal_color = "Set3", 
    title = "Weekly hospitalizations due to COVID-19 (data and forecasts)"
  )

Warning: ! `model_out_tbl` must be a `model_out_tbl`. Class applied by default

Warning: ! `model_out_tbl` contains more than 5 models, the plot will be reduced to show
  only one interval (the maximum interval value): "0.95"

Warning: ! `output_type_id` column must be a numeric. Converting to numeric.

Tip

Take a moment to explore the forecasts interactively in the above plot. We suggest starting by double-clicking on the “target” line in the legend. This will remove all models from the plot. Then add the models one at a time to compare them.

Who submitted when?

One thing that can foul up evaluation and ensembles of models is when not all models submit at the same times.

Do all models in our dataset of forecasts have the same number of predictions? Let’s look at this a few different ways.

Here is a tabular summary showing some summary stats about how often and how much each model submitted:

covid_forecasts |> 
  group_by(model_id) |> 
  summarise(
    n_submissions = n_distinct(reference_date),
    n_rows = n(),
    n_horizons = n_distinct(horizon),
    n_locations = n_distinct(location)
  ) |> 
  arrange(-n_submissions) |> 
  knitr::kable()

model_id	n_submissions	n_rows	n_horizons	n_locations
CEPH-Rtrend_covid	33	160908	4	53
CovidHub-baseline	33	160908	4	53
CovidHub-ensemble	33	160908	4	53
CMU-TimeSeries	32	156032	4	53
CMU-climate_baseline	32	156032	4	53
UMass-ar6_pooled	32	155112	4	53
UMass-gbqr	32	155112	4	53
OHT_JHU-nbxd	31	151156	4	53
MOBS-GLEAM_COVID	29	136068	4	52
UM-DeepOutbreak	27	131652	4	53
CFA_Pyrenew-Pyrenew_H_COVID	26	59202	2	51
NEU_ISI-AdaptiveEnsemble	26	104995	4	53
Metaculus-cp	22	966	4	1
CFA_Pyrenew-Pyrenew_HE_COVID	19	43746	2	51
JHU_CSSE-CSSE_Ensemble	19	82340	4	52
CFA_Pyrenew-Pyrenew_HW_COVID	18	31694	2	48
UGA_flucast-INFLAenza	16	78016	4	53
Google_SAI-Ensemble	12	58144	4	53
CFA_Pyrenew-PyrenewHEW_COVID	11	19642	2	47

And here is a visual showing more details about submissions each week by model, sorted with the models with the most forecasts at the top. Each tile represents a week, with lighter blue colors in a given model-week indicating a higher number of locations being submitted for.

covid_forecasts |> 
  group_by(model_id, reference_date) |> 
  summarise(
    n_rows = n(),
    n_locations = n_distinct(location)
  ) |> 
  ungroup() |> 
  mutate(model_id = reorder(model_id, n_rows, FUN = sum)) |> 
  ggplot() +
  geom_tile(aes(x = reference_date, y = model_id, fill = n_locations))

`summarise()` has grouped output by 'model_id'. You can override using the
`.groups` argument.

Take 2 minutes

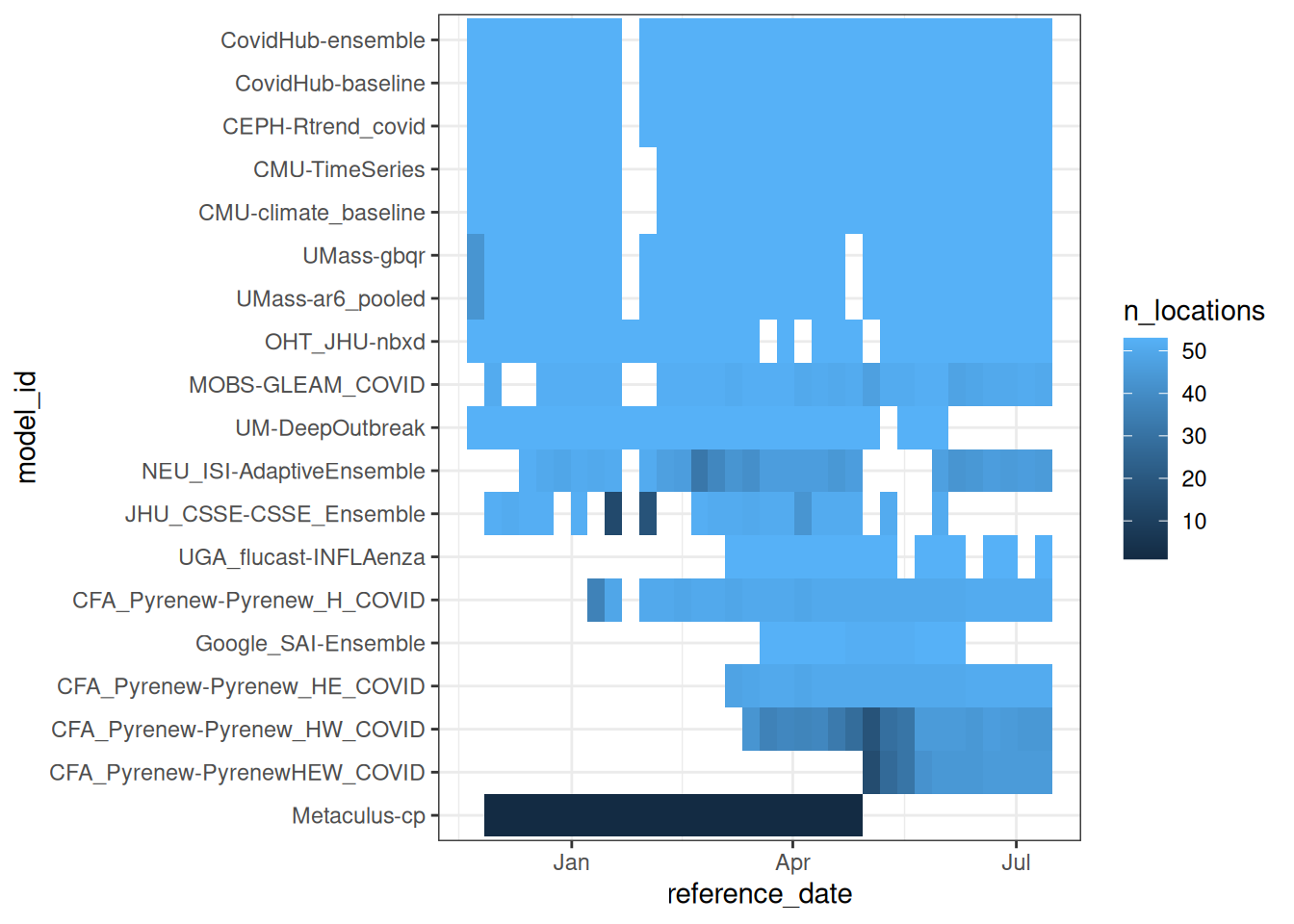
What are some reasons you can imagine for a model not being submitted in a given week?

Solution

Here are some real examples of why models have not been submitted in a given week:

The target dataset is not released (as was the case one week in January 2025).
The modeler who runs the model every week is sick or on vacation.
A model may have joined mid-season because it was still in development.
A model have have gone offline because a team stopped participating.
The modeling team may be unhappy with their forecast and decide not to submit (for evaluation of the model vs the modeling team this can be a big problem).
… (there are likely other reasons too)

What are the models?

What is a baseline model?

Baseline models generate forecasts that are created to serve as benchmarks. They are designed to be naive, not overly “optimized” approaches that make forecasts. In evaluation, baseline models may occasionally do well by chance (for example, a flat line model may do well when dynamics are, well, flat). But in general, their forecasts should be “beatable” by models that are able to learn and make predictions based on dynamics in the data. The Random Walk (rw) model from the Forecast Evaluation session is a good example of a baseline model. Other models that might serve as slightly more sophisticated forecast baselines could be a simple ARIMA model, or a model that smooths the recent data and predicts the a continuation of a recent trend in the data.

You can read about each of the models in the model-metadata folder of the forecast hub. Model metadata can also be programmatically accessed using hubData::load_model_metadata(). There are a wide variety of models submitted to this hub.

Tip

Here are a few models that we will highlight with their provided descriptions before going further:

This is the hub-generated ensemble forecast:

CovidHub-ensemble: “Median-based ensemble of quantile forecasts submissions.” Note this is similar to the ensembles we introduced in the ensembles session.

Here are two models that have been explicitly designed as “baselines” or benchmarks:

CovidHub-baseline: Flat baseline model. The most observed value from the target dataset is the median forward projection. Prospective uncertainty is based on the preceding timeseries.” (This is kind of like the rw model from previous sessions.)
CMU-climate_baseline: “Using data from 2022 onwards, the climatological model uses samples from the 7 weeks centered around the target week and reference week to form the quantiles for the target week, as one might use climate information to form a meteorological forecast. To get more variation at some potential issue of generalization, one can form quantiles after aggregating across geographic values as well as years (after converting to a rate based case count). This model uses a simple average of the geo-specific quantiles and the geo-aggregated quantiles.” (This is kind of like our fourier model from previous sessions.)

Here are two models built by InsightNet-funded teams:

UMass-ar6_pooled: “AR(6) model after fourth root data transform. AR coefficients are shared across all locations. A separate variance parameter is estimated for each location.”
MOBS-GLEAM_COVID: “Metapopulation, age structured SLIR model. … The GLEAM framework is based on a metapopulation approach in which the US is divided into geographical subpopulations. Human mobility between subpopulations is represented on a network. … Superimposed on the US population and mobility layers is an compartmental epidemic model that defines the infection and population dynamics.”

Take 2 minutes

Browse through some of the other model descriptions. Which ones look interesting to you and why? Discuss with your neighbor.

Evaluating forecasts

To quantitatively evaluate the forecasts, we will need the “oracle output” data. Recall that this is the “ground truth” (or target) data, formatted like it were being predicted by a future-seeing model. Here is code to build oracle-output data from the time-series target data.

covid_oracle_output <- covid_time_series |> 
  filter(as_of == as.Date("2025-07-09")) |> 
  select(target,
         location,
         target_end_date = date,
         oracle_value = observation)

Visual evaluation

Even though we have probabilistic forecasts, sometimes it is just easier to look at the point forecasts when trying to look at a lot of forecasts. Here is a plot showing all the point forecasts (the median from the quantile forecasts) for one state. The forecasts are in red and the black line shows the observed data.

covid_forecasts |> 
  filter(output_type_id == 0.5,
         abbreviation == "GA") |> 
  ggplot() +
  geom_line(aes(x = target_end_date, 
                y = value, 
                group = interaction(reference_date, model_id)),
            alpha = 0.5, 
            color = "red") +
  geom_line(data = filter(covid_time_series, 
                          abbreviation == "GA",
                          as_of == "2025-07-09"), 
            aes(x = date,
                y = observation))+
  ggtitle("Forecasts and data for Georgia") +
  ylab("incident hospital admissions") +
  xlab(NULL)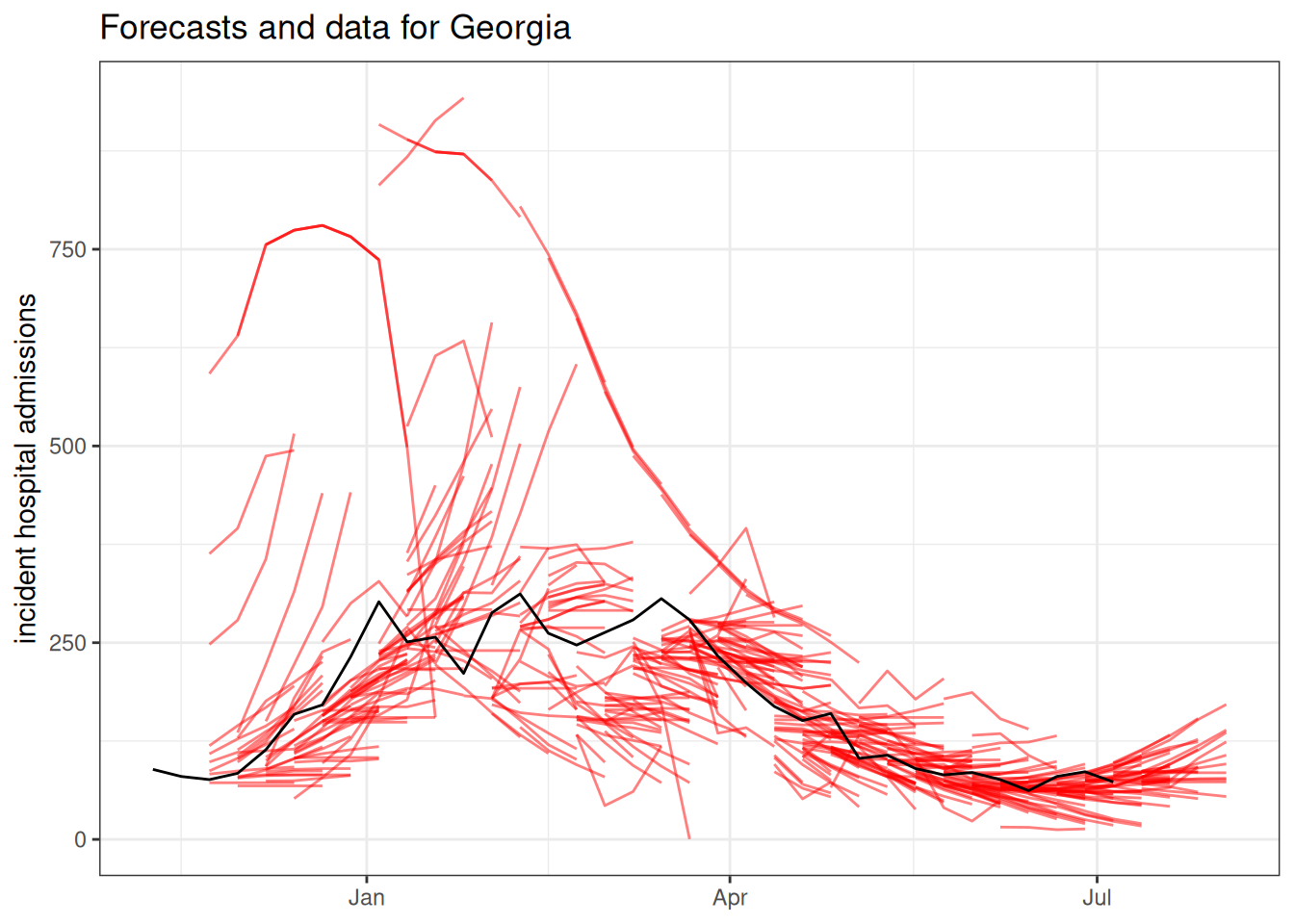

covid_forecasts |> 
  filter(output_type_id == 0.5,
         abbreviation == "VA") |> 
  ggplot() +
  geom_line(aes(x = target_end_date, 
                y = value, 
                group = interaction(reference_date, model_id)),
            alpha = 0.5, 
            color = "red") +
  geom_line(data = filter(covid_time_series, 
                          abbreviation == "VA",
                          as_of == "2025-07-09"), 
            aes(x = date,
                y = observation))+
  ggtitle("Forecasts and data for Virginia") +
  ylab("incident hospital admissions") +
  xlab(NULL)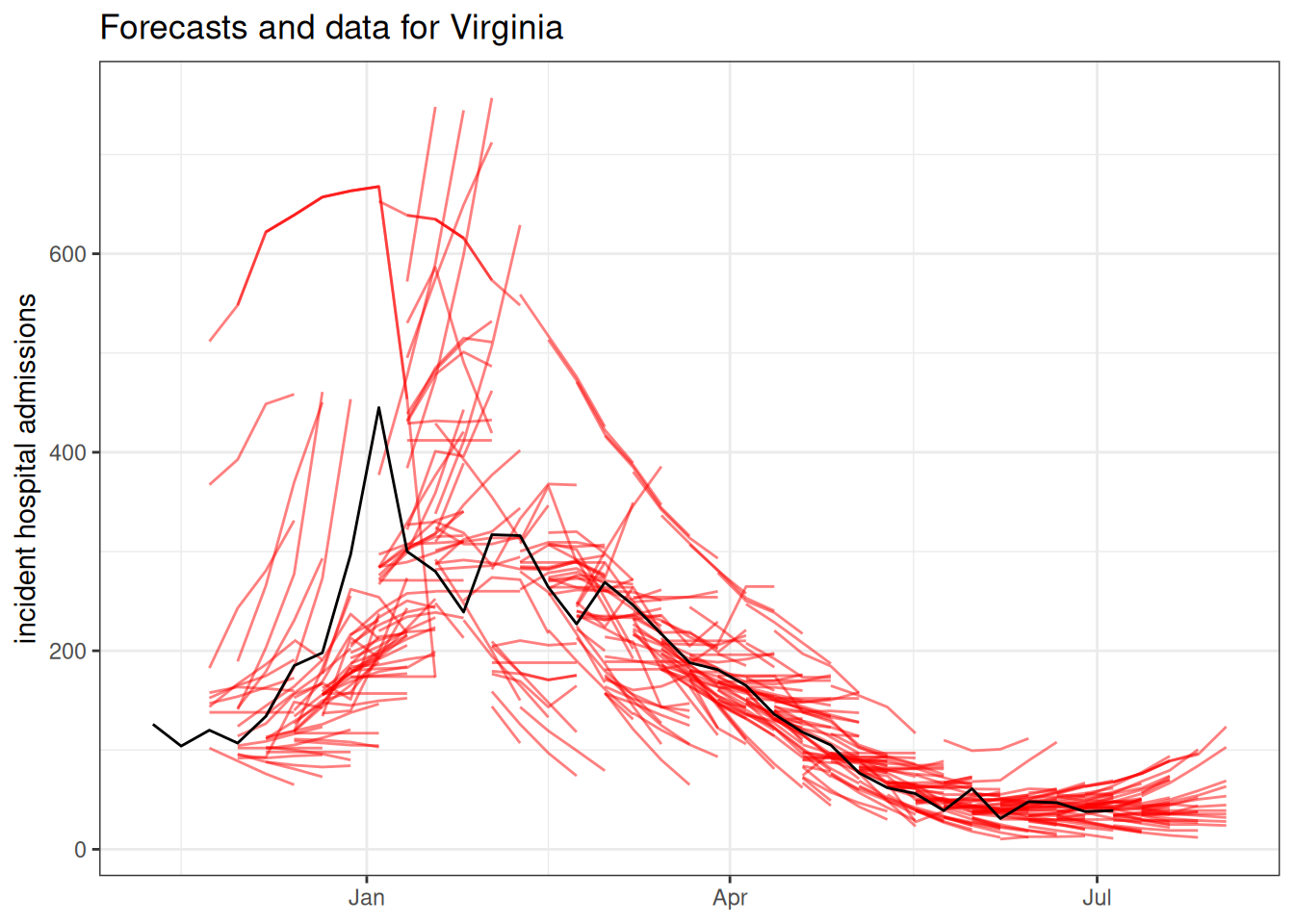

The forecasts can be interactively explored at the COVID-19 Forecast Hub Dashboard.

Overall model comparison

We will start our quantitative analysis with an overall evaluation of the models, using, as we did in earlier sessions, hubEvals. We will use the Weighted Interval Score (WIS) as our primary metric of interest as we did in the session on Forecast Ensembles.

scores <- score_model_out(
  covid_forecasts, 
  covid_oracle_output
  )

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

scores |> 
  arrange(wis) |> 
  knitr::kable(digits = 3)

model_id	wis	overprediction	underprediction	dispersion	bias	interval_coverage_50	interval_coverage_90	ae_median
CFA_Pyrenew-PyrenewHEW_COVID	7.566	2.740	1.690	3.136	0.069	0.503	0.875	11.987
CFA_Pyrenew-Pyrenew_HW_COVID	11.988	1.551	4.163	6.275	-0.127	0.575	0.932	17.033
CFA_Pyrenew-Pyrenew_HE_COVID	15.643	3.957	4.749	6.937	-0.033	0.511	0.887	23.709
UGA_flucast-INFLAenza	19.607	4.729	5.098	9.779	0.084	0.531	0.910	30.682
Google_SAI-Ensemble	25.710	7.096	12.936	5.678	-0.078	0.432	0.850	35.452
CFA_Pyrenew-Pyrenew_H_COVID	40.732	8.706	15.243	16.782	-0.205	0.530	0.898	62.741
CovidHub-ensemble	41.166	6.813	14.184	20.169	-0.100	0.561	0.909	62.543
UMass-ar6_pooled	47.129	11.030	16.047	20.051	0.023	0.576	0.916	70.351
UMass-gbqr	51.002	6.195	30.430	14.377	-0.100	0.459	0.836	74.142
CEPH-Rtrend_covid	52.582	7.454	21.806	23.322	-0.231	0.463	0.825	81.899
OHT_JHU-nbxd	57.426	6.205	36.073	15.148	-0.212	0.349	0.685	86.601
CovidHub-baseline	59.678	11.839	27.006	20.833	-0.070	0.627	0.848	80.823
NEU_ISI-AdaptiveEnsemble	59.836	20.368	19.107	20.361	-0.079	0.357	0.700	92.284
CMU-TimeSeries	63.432	23.031	9.323	31.078	-0.052	0.508	0.900	92.438
JHU_CSSE-CSSE_Ensemble	64.317	19.601	18.537	26.179	-0.068	0.485	0.811	91.388
MOBS-GLEAM_COVID	64.494	13.450	35.783	15.261	-0.349	0.303	0.638	96.427
UM-DeepOutbreak	71.665	15.181	13.954	42.530	0.008	0.639	0.940	96.881
CMU-climate_baseline	130.380	61.793	3.076	65.511	0.455	0.492	0.934	229.489
Metaculus-cp	1315.161	77.497	281.803	955.862	-0.190	0.690	1.000	1657.442

Take 2 minutes

Should we trust the results in this table to give us a reliable ranking for all of the forecasts? Why or why not?

Solution

Because there are so many missing forecasts, this single summary is not reliable. We will need a more careful comparison to determine relative rankings of models.

Recall, here is the summary of which models submitted when. There is a lot of variation in how much each model submitted!

covid_forecasts |> 
  group_by(model_id) |> 
  summarise(
    n_submissions = n_distinct(reference_date),
    n_rows = n(),
    n_horizons = n_distinct(horizon),
    n_locations = n_distinct(location)
  ) |> 
  arrange(-n_submissions) |> 
  knitr::kable()

model_id	n_submissions	n_rows	n_horizons	n_locations
CEPH-Rtrend_covid	33	160908	4	53
CovidHub-baseline	33	160908	4	53
CovidHub-ensemble	33	160908	4	53
CMU-TimeSeries	32	156032	4	53
CMU-climate_baseline	32	156032	4	53
UMass-ar6_pooled	32	155112	4	53
UMass-gbqr	32	155112	4	53
OHT_JHU-nbxd	31	151156	4	53
MOBS-GLEAM_COVID	29	136068	4	52
UM-DeepOutbreak	27	131652	4	53
CFA_Pyrenew-Pyrenew_H_COVID	26	59202	2	51
NEU_ISI-AdaptiveEnsemble	26	104995	4	53
Metaculus-cp	22	966	4	1
CFA_Pyrenew-Pyrenew_HE_COVID	19	43746	2	51
JHU_CSSE-CSSE_Ensemble	19	82340	4	52
CFA_Pyrenew-Pyrenew_HW_COVID	18	31694	2	48
UGA_flucast-INFLAenza	16	78016	4	53
Google_SAI-Ensemble	12	58144	4	53
CFA_Pyrenew-PyrenewHEW_COVID	11	19642	2	47

In real-world forecasting hubs, it is very common to have missing forecasts, and it probably isn’t safe to assume that these forecasts are “missing at random”. For example, some teams may choose not to submit forecasts when their model’s algorithm fails to converge, signaling a particularly difficult phase of the outbreak to predict—while others, consciously or not, submit during these periods and receive lower scores.

Additional metrics

Before we dig further into the evaluation, let’s introduce a few additional evaluation metrics and ideas.

Relative scores

Relative skill scores are a way to create “head-to-head” comparisons of models that to some extent are able to adjust for the difficulty of the predictions made by each model. Here is a figure showing how the relative scores are calculated, based on aggregated pairwise comparisons between each pair of models.

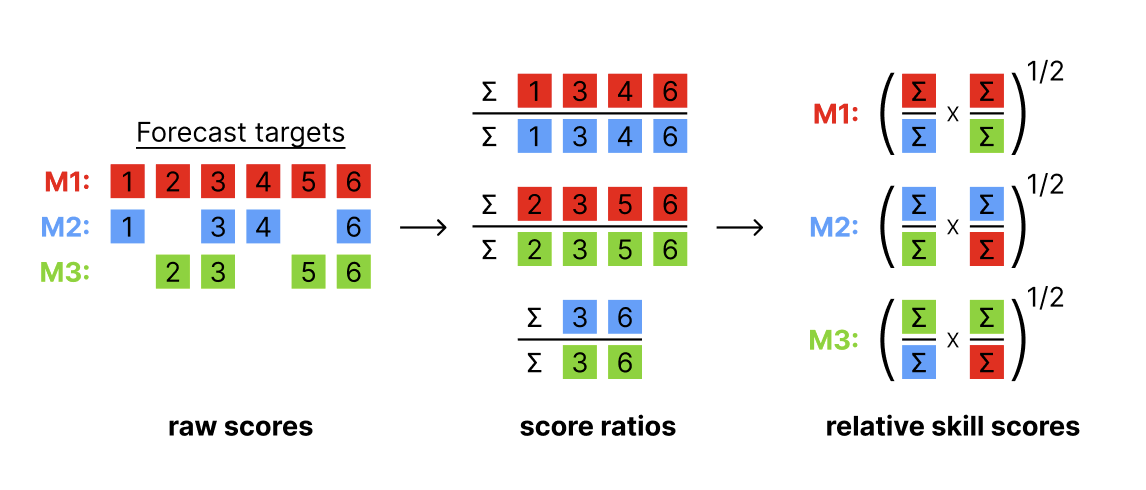
Schematic of relative skill score computation.(Bosse et al. 2024)

Interpreting relative skill

The interpretation of the relative skill metric is the factor by which the score for a given model is more or less accurate than the average model, adjusting for the difficulty of the forecasts made by that particular model. Relative skill scores that are lower than 1 indicate that the model is more accurate on the whole than the average model evaluated. For example, a 0.9 relative WIS skill for model A suggests that model A was 10% more accurate on average than other models, adjusting for the difficulty level of forecasts made by model A.

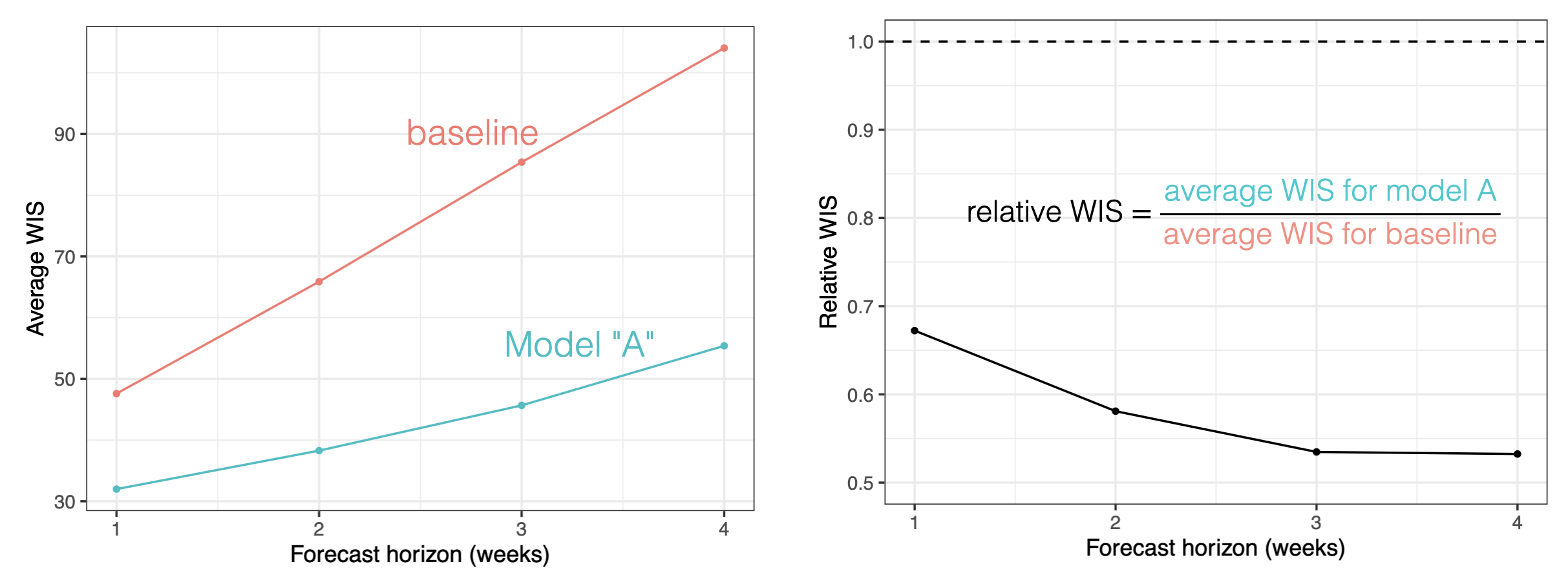
This metric (or a version of it) has been used in practice in a number of large-scale forecast evaluation research papers.(Cramer et al. 2022; Meakin et al. 2022; Sherratt et al. 2023; Wolffram et al. 2023) The general rule of thumb is that it does a reasonable job comparing models where there is never less than, say, 50% overlap in the targets predicted by any pair of models.

Here is a table of relative skill scores for WIS.

score_model_out(
  covid_forecasts, 
  covid_oracle_output,
  metrics = "wis",
  relative_metrics = "wis"
  ) |> 
  arrange(wis_relative_skill)

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

Warning in wilcox.test.default(values_x, values_y, paired = TRUE): cannot
compute exact p-value with ties

Key: <model_id>
                        model_id         wis wis_relative_skill
                          <char>       <num>              <num>
 1: CFA_Pyrenew-Pyrenew_HE_COVID   15.643224          0.6617223
 2:        UGA_flucast-INFLAenza   19.606728          0.6992593
 3:            CovidHub-ensemble   41.165853          0.7351364
 4: CFA_Pyrenew-PyrenewHEW_COVID    7.565851          0.7683668
 5:             UMass-ar6_pooled   47.128999          0.8615963
 6:                   UMass-gbqr   51.001652          0.9039621
 7:            CEPH-Rtrend_covid   52.582203          0.9575737
 8:     NEU_ISI-AdaptiveEnsemble   59.836005          0.9580200
 9:                 OHT_JHU-nbxd   57.425689          0.9616374
10:            CovidHub-baseline   59.678144          1.0116854
11:               CMU-TimeSeries   63.431791          1.0140982
12: CFA_Pyrenew-Pyrenew_HW_COVID   11.988136          1.0340812
13:                 Metaculus-cp 1315.160817          1.0370798
14:       JHU_CSSE-CSSE_Ensemble   64.317330          1.0621682
15:          Google_SAI-Ensemble   25.710362          1.0696303
16:  CFA_Pyrenew-Pyrenew_H_COVID   40.731989          1.1823656
17:             MOBS-GLEAM_COVID   64.493753          1.2589497
18:              UM-DeepOutbreak   71.664888          1.2608713
19:         CMU-climate_baseline  130.379998          2.3539375

Note that the ordering of the wis column does not align perfectly with the wis_relative_skill column. This is due to the “adjustment” of the relative skill based on which forecasts were made by each model.

To make a more fair comparison, let’s subset to only include models that have submitted at least 60% of the maximum possible number of predictions for the season.

## 33 dates, 4 horizons, 53 locations, 60%
threshold_60pct <- 33 * 4 * 53 * 0.6
model_subset <- covid_forecasts |> 
  filter(output_type_id == 0.5) |> 
  group_by(model_id) |> 
  summarize(targets = n()) |> 
  filter(targets > threshold_60pct) |> 
  pull(model_id)

covid_forecasts |> 
  filter(model_id %in% model_subset) |> 
  score_model_out(
    covid_oracle_output,
    metrics = "wis",
    relative_metrics = "wis"
  ) |> 
  arrange(wis_relative_skill)

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

Key: <model_id>
                    model_id       wis wis_relative_skill
                      <char>     <num>              <num>
 1:        CovidHub-ensemble  41.16585          0.6952576
 2:         UMass-ar6_pooled  47.12900          0.8067576
 3:               UMass-gbqr  51.00165          0.8734806
 4:        CEPH-Rtrend_covid  52.58220          0.8871788
 5: NEU_ISI-AdaptiveEnsemble  59.83600          0.8967471
 6:             OHT_JHU-nbxd  57.42569          0.9010345
 7:        CovidHub-baseline  59.67814          0.9715371
 8:           CMU-TimeSeries  63.43179          1.0355758
 9:          UM-DeepOutbreak  71.66489          1.0776110
10:         MOBS-GLEAM_COVID  64.49375          1.2025614
11:     CMU-climate_baseline 130.38000          2.1838601

Take 5 minutes

Looking at the relative and absolute WIS scores from the table above, and the number of total forecasts for each model, what are some of your take-aways from the analysis above?

Solution

The ensemble forecast is the most accurate model overall, by fairly large margin, close to 20% in terms of absolute WIS and 10% in terms of relative skill.
The CovidHub-baseline has basically “average” performance, with a relative WIS score of 0.96.
Five individual models have better performance than the baseline and four have worse performance than the baseline.
The worst-performing model is the CMU-climate_baseline. This is designed to be a “seasonal average” model, and covid isn’t that seasonal at the moment, so it’s not super surprising that this is a bad model.
Tying back to approaches from the Renewal equation session:
- The CEPH-Rtrend_covid model is “A renewal equation method based on Bayesian estimation of Rt from hospitalization data.” It wasn’t as good as pure statistical and ML approaches, but was better than the baseline.
- The MOBS-GLEAM_COVID model is a mechanistic model (see description above) and was worse than the baseline.

Since the counts at the national level are likely to dominate the absolute scale of average WIS scores, you could make an argument to subset to only the states and evaluate based on that. Here is the analysis above, on that subset:

covid_forecasts |> 
  filter(model_id %in% model_subset,
         location != "US") |> 
  score_model_out(
    covid_oracle_output,
    metrics = "wis",
    relative_metrics = "wis"
  ) |> 
  arrange(wis_relative_skill)

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

Key: <model_id>
                    model_id      wis wis_relative_skill
                      <char>    <num>              <num>
 1:        CovidHub-ensemble 25.64862          0.7289393
 2:         UMass-ar6_pooled 28.95864          0.8191001
 3:               UMass-gbqr 29.05540          0.8218274
 4:        CEPH-Rtrend_covid 31.83277          0.9039557
 5:        CovidHub-baseline 34.29734          0.9441114
 6:           CMU-TimeSeries 33.94338          0.9589511
 7:             OHT_JHU-nbxd 36.27410          0.9644199
 8: NEU_ISI-AdaptiveEnsemble 39.92454          1.0457292
 9:          UM-DeepOutbreak 41.43688          1.0521645
10:         MOBS-GLEAM_COVID 36.18229          1.1470630
11:     CMU-climate_baseline 71.84392          2.0458225

The results above haven’t changed much, although the CMU-TimeSeries and OHT_JHU-nbxd swapped places in the final rankings.

Log-scale scores

We can also score on the logarithmic scale. This can be useful if we are interested in the relative performance of the model at different scales of the data, for example if we are interested in the model’s performance at capturing the exponential growth phase of the epidemic.(Bosse et al. 2023) In some sense, scoring in this way can be an approximation of scoring the effective reproduction number estimates. Doing this directly can be difficult as the effective reproduction number is a latent variable and so we cannot directly score it. Additionally, it can make sense to score a target (and make it easier to compare scores) when the variance of the scores is stabilized.

To implement the log-scale scoring, we can simply log-transform the observations and forecasted values (with an offset, to account for zeroes in the data).

covid_forecasts |> 
  filter(model_id %in% model_subset) |> 
  mutate(value = log(value+1)) |> 
  score_model_out(
    covid_oracle_output |> 
      mutate(oracle_value = log(oracle_value+1)),
    metrics = "wis",
    relative_metrics = "wis"
  ) |> 
  arrange(wis_relative_skill)

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

Key: <model_id>
                    model_id       wis wis_relative_skill
                      <char>     <num>              <num>
 1:        CovidHub-ensemble 0.1935312          0.7189940
 2:               UMass-gbqr 0.2188057          0.8143009
 3:           CMU-TimeSeries 0.2228692          0.8209956
 4:         UMass-ar6_pooled 0.2285401          0.8474079
 5:        CEPH-Rtrend_covid 0.2588151          0.9592896
 6:             OHT_JHU-nbxd 0.2679237          0.9827550
 7: NEU_ISI-AdaptiveEnsemble 0.2619506          1.0265103
 8:        CovidHub-baseline 0.2922600          1.0798208
 9:         MOBS-GLEAM_COVID 0.2953681          1.1490552
10:          UM-DeepOutbreak 0.3609916          1.3719314
11:     CMU-climate_baseline 0.4036584          1.4902983

Note that this rescaling of the data prior to scoring results in a more substantial change in the evaluation. While the ensemble remains the most accurate model, now five models are better than the baseline, and the UMass-gbqr model is the most accurate individual model (just barely edging out the CMU-TimeSeries model.)

Prediction interval coverage

The above comparisons focus on WIS and relative WIS, but in our collaborations with federal, state, and local epidemiologists, we have often found that the metric of prediction interval coverage rates is a useful tool for communicating the reliability of a set of forecasts. Prediction interval coverage measures the fraction of prediction intervals at a given levels that cover the truth. For example, if a model is well-calibrated, 50% PIs should cover the truth around 50% of the time, 90% PIs should cover the truth 90% of the time, etc… This is a key part of the forecasting paradigm mentioned in the Forecast Evaluation session is that we want to maximize sharpness subject to calibration. Prediction interval coverage rates help assess calibration. Prediction interval widths can help assess sharpness.

Tip

Prediction interval coverage is not a proper score. For example, to get perfect 90% PI coverage, you could always make 9 out of every 10 of your intervals infinitely wide and the last one infinitely small. Et voila! 90% PI coverage achieved.

But, assuming that modelers aren’t trying to game the scores, it can generally be a useful and interpretable metric in practice. Let’s add some PI coverage metrics to our (unscaled) results from before.

covid_forecasts |> 
  filter(model_id %in% model_subset) |> 
  score_model_out(
    covid_oracle_output,
    metrics = c("wis", "interval_coverage_50", "interval_coverage_90")
  ) |> 
  arrange(interval_coverage_90) |> 
  knitr::kable(digits = 3)

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

model_id	wis	interval_coverage_50	interval_coverage_90
MOBS-GLEAM_COVID	64.494	0.303	0.638
OHT_JHU-nbxd	57.426	0.349	0.685
NEU_ISI-AdaptiveEnsemble	59.836	0.357	0.700
CEPH-Rtrend_covid	52.582	0.463	0.825
UMass-gbqr	51.002	0.459	0.836
CovidHub-baseline	59.678	0.627	0.848
CMU-TimeSeries	63.432	0.508	0.900
CovidHub-ensemble	41.166	0.561	0.909
UMass-ar6_pooled	47.129	0.576	0.916
CMU-climate_baseline	130.380	0.492	0.934
UM-DeepOutbreak	71.665	0.639	0.940

These results are sorted by the 90% PI coverage, but note that lower is not necessarily “better” here. What is good is having interval_coverage_90 scores that are close to 0.90. A few models (CMU-TimeSeries and CMU-climate_baseline) all have coverage rates within 5% of the nominal level for both 50% and 90% PIs.

Tip

Note, this is a nice example of a model (CMU-climate_baseline) being well calibrated (near-nominal PI coverage) but not having good accuracy (bad/high WIS on average).

Model comparison by horizon and forecast date

As we discussed in the session on evaluating forecasts, overall comparisons can miss details about ways that models perform across different forecast dimensions. Let’s run an analysis looking at the performance of model by horizon and then by forecast date. For now, we will keep the focus on the 10 models that made at least 60% of possible predictions, and we will only evaluate state-level forecasts.

scores_by_horizon <- covid_forecasts |> 
  filter(model_id %in% model_subset,
         location != "US") |> 
  score_model_out(
    covid_oracle_output,
    metrics = "wis",
    relative_metrics = "wis",
    by = c("model_id", "horizon")
  )

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

p <- ggplot(scores_by_horizon)+
  geom_line(aes(x = horizon, y = wis, color = model_id))
plotly::ggplotly(p)

For looking by reference_date, we will also plot the relative WIS.

scores_by_reference_date <- covid_forecasts |> 
  filter(model_id %in% model_subset,
         location != "US") |> 
  score_model_out(
    covid_oracle_output,
    metrics = "wis",
    relative_metrics = "wis",
    by = c("model_id", "reference_date")
  ) |> 
  tidyr::pivot_longer(cols = c(wis, wis_relative_skill), 
                      names_to = "metric",
                      values_to = "score")

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

p <- ggplot(scores_by_reference_date)+
  geom_line(aes(x = reference_date, y = score, color = model_id)) +
  facet_grid(metric~., scales = "free_y")
plotly::ggplotly(p)

Take 5 minutes

By horizon and reference date, how variable are the models in their accuracy?

Solution

In general, the models seem fairly consistent in their performance. There are few “crossings” in the by horizon plot, suggesting that by and large models that are accurate at short-term horizons are also accurate at the longer horizons. There is much more variability by date, although it still seems that with a few exceptions, models aren’t jumping around too dramatically in their relative (or absolute level) WIS.

Ensembling forecasts

In this section, we will build several new ensemble forecasts and compare these to the CovidHub-ensemble model. Based on the last results from the section above, we saw that there was some fairly consistent performance from a few of the models. This is one precondition for weighted ensembles to have a chance at performing well. Here are the different approaches we will use:

lop_unweighted_all: an unweighted linear opinion pool (LOP) of all available forecasts each week.
lop_unweighted_select: an unweighted LOP of the most commonly submitted forecasts.
lop_inv_wis_weighted_select: a weighted LOP of the most commonly submitted forecasts.
median_inv_wis_weighted_select: a weighted median ensemble of the most commonly submitted forecasts.

Note that the existing CovidHub-ensemble forecast is basically median-unweighted-all in the above nomenclature. It would be hard to do any weighted-all ensembles since when models are missing a lot of forecasts it might be hard to estimate an accurate weight for them.

Build unweighted LOP ensembles

Let’s start with the “easy” part, building the unweighted ensembles.

LOP details

Note that when we build LOPs with quantile based forecasts, the algorithm needs to approximate a full distribution (the tails are not well-defined in a quantile representation). There are some assumptions made under the hood about how this is approximated. For the really gory details, you can check out the hubEnsembles documentation

Note that trying to build all of the forecasts in one call to linear_pool() exceeded the memory on your instructors laptop, so we will do a purrr::map_dfr() “loop” to do this one reference_date at a time. (This code takes a few minutes to run.)

# Get a list of unique reference dates, removing the last one
reference_dates <- covid_forecasts |> 
  filter(reference_date != as.Date("2025-07-12")) |> 
  pull(reference_date) |> 
  unique()

# Map over each date and apply linear_pool separately
lop_unweighted_all <- purrr::map_dfr(
  reference_dates, 
  function(date) {
    covid_forecasts |> 
      filter(model_id != "CovidHub-ensemble", 
             reference_date == date) |> 
      hubEnsembles::linear_pool(model_id = "lop_unweighted_all")
})


lop_unweighted_select <- purrr::map_dfr(
  reference_dates, 
  function(date) {
    covid_forecasts |> 
      filter(model_id %in% model_subset,
             model_id != "CovidHub-ensemble", 
             reference_date == date) |> 
      hubEnsembles::linear_pool(model_id = "lop_unweighted_select")
})

Build weighted ensemble

Inverse WIS weighting is a simple method that weights the forecasts by the inverse of their WIS over some period. Note that identifying what this period should be in order to produce the best forecasts is not straightforward as predictive performance may vary over time if, say, some models are better at making predictions during different parts of an outbreak. For example, some models might be good at predicting exponential growth at the beginning of an outbreak but not as good at seeing the slowdown.

The main benefit of WIS weighting over other methods is that it is simple to understand and implement. However, it does not optimise the weights directly to produce the best forecasts. It relies on the hope that giving more weight to better performing models yields a better ensemble.

We will use the WIS scores that we have computed above to generate weights for our ensembles. The weights for one reference_date will be based on the inverse of the cumulative average WIS achieved by the model up to the week prior to the current reference_date.

Caution

Note that since our scores are computed based on data available at the end of the season, this is kind of “cheating”, since we’re using information that would not have been available to us in real time. If we were to do this entirely correctly, we would, for each week, compute the scores based on the available data at that time.

Let’s start by calculating WIS values by model and target_end_date. This will allow us to see what scores are available for a model’s forecasts that it had for dates prior to the current forecast date.

scores_by_target_date <- covid_forecasts |> 
  filter(model_id %in% model_subset,
         location != "US") |> 
  score_model_out(
    covid_oracle_output,
    metrics = "wis",
    by = c("model_id", "target_end_date")
  )

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

scores_by_target_date

              model_id target_end_date       wis
                <char>          <Date>     <num>
  1: CEPH-Rtrend_covid      2024-11-23 26.908679
  2: CEPH-Rtrend_covid      2024-11-30 28.499946
  3: CEPH-Rtrend_covid      2024-12-07 30.215181
  4: CEPH-Rtrend_covid      2024-12-14 31.887136
  5: CEPH-Rtrend_covid      2024-12-21 36.592749
 ---                                            
352:        UMass-gbqr      2025-06-07 11.916627
353:        UMass-gbqr      2025-06-14 12.991709
354:        UMass-gbqr      2025-06-21 12.173811
355:        UMass-gbqr      2025-06-28 10.808055
356:        UMass-gbqr      2025-07-05  9.590668

Now, we will compute a cumulative average WIS up to a given date for all models except the ensemble, which we are not going to include in our ensemble.

cum_wis <- scores_by_target_date |>
  filter(model_id != "CovidHub-ensemble") |> 
  arrange(model_id, target_end_date) |> 
  group_by(model_id) |> 
  mutate(
    cumulative_mean_wis = cummean(wis), ## cumulative mean WIS including current week
    cumulative_mean_wis_lag1 = lag(cumulative_mean_wis)
    ) |> 
  ungroup()
cum_wis

# A tibble: 323 × 5
   model_id     target_end_date   wis cumulative_mean_wis cumulative_mean_wis_…¹
   <chr>        <date>          <dbl>               <dbl>                  <dbl>
 1 CEPH-Rtrend… 2024-11-23       26.9                26.9                   NA  
 2 CEPH-Rtrend… 2024-11-30       28.5                27.7                   26.9
 3 CEPH-Rtrend… 2024-12-07       30.2                28.5                   27.7
 4 CEPH-Rtrend… 2024-12-14       31.9                29.4                   28.5
 5 CEPH-Rtrend… 2024-12-21       36.6                30.8                   29.4
 6 CEPH-Rtrend… 2024-12-28       61.6                36.0                   30.8
 7 CEPH-Rtrend… 2025-01-04       89.2                43.6                   36.0
 8 CEPH-Rtrend… 2025-01-11       52.2                44.6                   43.6
 9 CEPH-Rtrend… 2025-01-18       65.7                47.0                   44.6
10 CEPH-Rtrend… 2025-01-25       91.7                51.4                   47.0
# ℹ 313 more rows
# ℹ abbreviated name: ¹cumulative_mean_wis_lag1

Tip

Note that we also compute a cumulative_mean_wis_lag1, which is the mean up through the previous week. This is to inject a bit of realism: how could we know in real-time how our forecast did for the current week?

So the cumulative_mean_wis_lag1 is the cumulative mean WIS that we could have observed at the target_end_date. (This all still assumes that whatever data we observed at the target_end_date was complete and never revised.)

We will proceed by computing the inverse mean wis and using those to derive the weights.

weights_per_model <- cum_wis |> 
  mutate(inv_wis = 1 / cumulative_mean_wis_lag1) |>
  group_by(target_end_date) |> 
  mutate(inv_wis_total_by_date = sum(inv_wis, na.rm = TRUE)) |>
  ungroup() |> 
  mutate(weight = inv_wis / inv_wis_total_by_date) |> ## this normalises the weights to sum to 1
  select(model_id, target_end_date, weight)

And we will put in place a few small fixes to the weights:

assign equal weights for the first two weeks. (There are missing forecasts here, and we haven’t learned much about the model performance yet anyways.)
change target_end_date to reference_date because now we want the weights computed up to that target_end_date to be applied on that reference_date.
set to 0 a missing weight for the NEU_ISI-AdaptiveEnsemble.

## assign equal weights for the first week
first_week_idx <- weights_per_model$target_end_date == as.Date("2024-11-23")
weights_per_model[first_week_idx, "weight"] <- 1/sum(first_week_idx)

second_week_idx <- weights_per_model$target_end_date == as.Date("2024-11-30")
weights_per_model[second_week_idx, "weight"] <- 1/sum(second_week_idx)

weights_per_model <- rename(weights_per_model, reference_date = target_end_date)

weights_per_model$weight[is.na(weights_per_model$weight)] <- 0

As always, it is good to plot your data as a sanity check. Here are the model weights plotted over time. For each week (x-axis), the weights assigned to each model are shown in a stacked bar plot, with the height of the bar equal to the weight of the model.

plot_weights <- ggplot(weights_per_model) +
  geom_col(aes(x = reference_date, y = weight, fill = model_id))
plotly::ggplotly(plot_weights)

Take 5 minutes

Looking at the above plot, what is the “story” that the weights tell when plotted over time? Which models did the ensemble like and dislike over time and how did it change? (Remember, in the first two weeks, all models received equal weight.)

Solution

Starting in the third week, three models were assigned less weight than others: CMU-climate-baseline, CMU-TimeSeries and COVIDHub-baseline. Over time, CMU-TimeSeries and COVIDHub-baseline earned back some “trust” with higher weights, but CMU-climate-baseline stayed with a low weight.

In general, the weights did not change much after the first few weeks (except in the last week when UM-DeepOutbreak wasn’t submitted.)

Now that we have the weights and we’ve checked them, let’s start building some ensembles! First, we will build the median ensembles, both weighted and unweighted..

## build the weighted ensemble
median_inv_wis_weighted_select <- covid_forecasts |> 
  filter(model_id %in% model_subset,
         model_id != "CovidHub-ensemble") |> 
  simple_ensemble(weights = weights_per_model, 
                  agg_fun = median,
                  model_id = "median_inv_wis_weighted_select")

## build unweighted select median ensemble
median_unweighted_select <- covid_forecasts |> 
  filter(model_id %in% model_subset,
         model_id != "CovidHub-ensemble") |> 
  simple_ensemble(agg_fun = median,
                  model_id = "median_unweighted_select")

And then we will build the inverse WIS weighted LOP ensemble.

Caution

It takes several minutes for the LOP ensembles to be built if you are running the code on your machine.

lop_inv_wis_weighted_select <- purrr::map_dfr(
  reference_dates, 
  function(date) {
    covid_forecasts |> 
      filter(model_id %in% model_subset,
             model_id != "CovidHub-ensemble", 
             reference_date == date) |> 
      linear_pool(model_id = "lop_inv_wis_weighted_select",
                  weights = weights_per_model)
})

Compare all ensembles

We will compare the performance of all ensembles just at the state level, since the scores by reference date were only computed at the state level.

covid_forecasts_w_ensembles <- bind_rows(
  covid_forecasts,
  lop_unweighted_all,
  lop_unweighted_select,
  lop_inv_wis_weighted_select,
  median_inv_wis_weighted_select,
  median_unweighted_select
)

model_subset_ens <- c("CovidHub-ensemble", 
                      "lop_unweighted_all",
                      "lop_unweighted_select",
                      "median_inv_wis_weighted_select",
                      "median_unweighted_select",
                      "lop_inv_wis_weighted_select")

covid_forecasts_w_ensembles |> 
  filter(model_id %in% model_subset_ens,
         location != "US") |> 
  score_model_out(
    covid_oracle_output
  ) |> 
  arrange(wis) |> 
  knitr::kable(digits = 2)

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

model_id	wis	overprediction	underprediction	dispersion	bias	interval_coverage_50	interval_coverage_90	ae_median
CovidHub-ensemble	25.65	4.67	9.96	11.02	-0.10	0.56	0.91	38.71
median_unweighted_select	25.77	4.62	9.08	12.08	-0.06	0.60	0.92	38.47
median_inv_wis_weighted_select	26.85	5.09	9.88	11.87	-0.07	0.59	0.91	40.34
lop_unweighted_all	27.15	3.38	7.76	16.00	-0.06	0.68	0.99	38.06
lop_inv_wis_weighted_select	27.21	3.38	9.01	14.82	-0.09	0.65	0.97	38.93
lop_unweighted_select	27.32	3.34	7.84	16.14	-0.06	0.68	0.99	38.22

Remember, in the above table, the CovidHub-ensemble is kind of like median-unweighted-all because it uses a median ensemble of all models available in every week without weights. Overall, the ensembles have fairly similar average WIS values across all dates and states. Using a median unweighted ensemble of frequently submitting models marginally outperformed the actual CovidHub-ensemble.

Take 5 minutes

Why do you think weighting does not improve the forecasts more?

Seeing these patterns, and the plots of the weights above, is there anything you might change if you were given the opportunity to compute the weights in a different way?

Write down your thoughts about these questions and compare answers with a neighbor.

Solution

Why aren’t weighted ensembles better?

When model performance varies a lot from one week to the next, it may be hard to estimate/anticipate/predict which model should get more weight in a given week.

What might your consider changing about the weights?

There isn’t one right answer here, but some things that you might consider to do differently are:

Figuring out a way to encourage the model to stay closer to equal weights early on. The weights are being perhaps overly influenced by small sample sizes there.
Thinking about using a rolling window of mean WIS to compute weights rather than overall cumulative. This could be good, but also assumes that recent performance will predict future performance, which is not always true!

It does not seem like weighting adds a lot of value to these forecasts, although perhaps with additional data on model performance the weights could be improved.

We can also look at how the ensemble performance varied over time.

ensemble_scores_by_reference_date <- covid_forecasts_w_ensembles |> 
  filter(model_id %in% model_subset_ens,
         location != "US") |> 
  score_model_out(
    covid_oracle_output,
    metrics = "wis",
    by = c("model_id", "reference_date")
  )

ℹ Some rows containing NA values may be removed. This is fine if not
  unexpected.

p <- ggplot(ensemble_scores_by_reference_date) +
  geom_line(aes(x = reference_date, y = wis, color = model_id))
plotly::ggplotly(p)

It is interesting to note how while the LOP ensembles did slightly worse overall, they actually had slightly more accurate forecasts near the peak of the season, especially in the weeks where the scores were the highest.

Going further

Challenge

Once you start looking at lots of plots of forecast scores, it is easy to fall into the trap of not looking at the actual forecasts. Looking at the scores of the ensemble forecasts by date, it looks like there was one week when the CovidHub-ensemble did much worse than other forecasts. Investigate this week in particular. What did the forecasts look like that week and what was anomalous about it?
In the evaluation of the real-world models, we subset to only models that had submitted a large fraction of forecasts. But this omits some interesting models, including the model from Metaculus, a human-judgment forecast aggregation company, and some models from the CDC Center for Forecasting and Outbreak Analytics (CFA). Adapt the code above to conduct a targeted and fair evaluation of the forecasts made by those models.
Look at the list of hubverse-style hubs. Using the code above, try to replicate some of the analyses in this session for a different hub. What challenges and obstacles do you run into?

Methods in practice

Ray et al. (2023) evaluates the performance of ensemble forecasts (including some weighted ensembles) in predicting COVID-19 cases, hospitalization and deaths, both with weighted and unweighted ensembles.
Sherratt et al. (2023) investigates the performance of different ensembles in the European COVID-19 Forecast Hub.

Wrap up

Review what you’ve learned in this session with the learning objectives

References

Bosse, Nikos I., Sam Abbott, Anne Cori, Edwin van Leeuwen, Johannes Bracher, and Sebastian Funk. 2023. “Scoring Epidemiological Forecasts on Transformed Scales.” Edited by James M McCaw. PLOS Computational Biology 19 (8): e1011393. https://doi.org/10.1371/journal.pcbi.1011393.

Bosse, Nikos I., Hugo Gruson, Anne Cori, Edwin van Leeuwen, Sebastian Funk, and Sam Abbott. 2024. “Evaluating Forecasts with Scoringutils in R.” arXiv. https://doi.org/10.48550/arXiv.2205.07090.

Cramer, Estee Y., Evan L. Ray, Velma K. Lopez, Johannes Bracher, Andrea Brennen, Alvaro J. Castro Rivadeneira, Aaron Gerding, et al. 2022. “Evaluation of Individual and Ensemble Probabilistic Forecasts of COVID-19 Mortality in the United States.” Proceedings of the National Academy of Sciences 119 (15): e2113561119. https://doi.org/10.1073/pnas.2113561119.

Fox, Spencer J., Minsu Kim, Lauren Ancel Meyers, Nicholas G. Reich, and Evan L. Ray. 2024. “Optimizing Disease Outbreak Forecast Ensembles.” Emerging Infectious Diseases 30 (9): 1967–69. https://doi.org/10.3201/eid3009.240026.

Kim, Minsu, Evan L. Ray, and Nicholas G. Reich. 2024. “Beyond Forecast Leaderboards: Measuring Individual Model Importance Based on Contribution to Ensemble Accuracy.” arXiv. https://doi.org/10.48550/arXiv.2412.08916.

Meakin, Sophie, Sam Abbott, Nikos Bosse, James Munday, Hugo Gruson, Joel Hellewell, Katharine Sherratt, et al. 2022. “Comparative Assessment of Methods for Short-Term Forecasts of COVID-19 Hospital Admissions in England at the Local Level.” BMC Medicine 20 (1): 86. https://doi.org/10.1186/s12916-022-02271-x.

Ray, Evan L., Logan C. Brooks, Jacob Bien, Matthew Biggerstaff, Nikos I. Bosse, Johannes Bracher, Estee Y. Cramer, et al. 2023. “Comparing Trained and Untrained Probabilistic Ensemble Forecasts of COVID-19 Cases and Deaths in the United States.” International Journal of Forecasting 39 (3): 1366–83. https://doi.org/10.1016/j.ijforecast.2022.06.005.

Sherratt, Katharine, Hugo Gruson, Rok Grah, Helen Johnson, Rene Niehus, Bastian Prasse, Frank Sandmann, et al. 2023. “Predictive Performance of Multi-Model Ensemble Forecasts of COVID-19 Across European Nations.” Edited by Amy Wesolowski, Neil M Ferguson, Jeffrey L Shaman, and Sen Pei. eLife 12 (April): e81916. https://doi.org/10.7554/eLife.81916.

Wolffram, Daniel, Sam Abbott, Matthias an der Heiden, Sebastian Funk, Felix Günther, Davide Hailer, Stefan Heyder, et al. 2023. “Collaborative Nowcasting of COVID-19 Hospitalization Incidences in Germany.” PLOS Computational Biology 19 (8): e1011394. https://doi.org/10.1371/journal.pcbi.1011394.